職業心理學第二章個性差異之量度

第二章個性差異之量度

　　吾人既已研究個性差異之原因，為研究職業心理學之背景，請再進而研究如何量度個性差異之程度。

　　量度個性差異之必要　吾人誠欲應用研究個性所得之結果，則在理論與實施各方面，對於一群內某種特性，或幾種特性，皆須求得一種量度之方法。而且有時不但量度而已，並須比較各種特性。誠欲從事比較，苟僅知某人所得關於某種特性之測驗分數較一群中之「平均」或「中數」多若干分，或少若干分；而未知此一群中各人測驗分數之差別情形，則此人在此一群中所處之地位（指程度），仍無明確之表示也。試舉一例以明之。例如此一群中受同一測驗者有百分之五十，其所得之分數與「平均」比較之數，皆與此人所得之比較結果相似，則此人之程度不能有所超出。如此一群中僅有百分之五，所有與「平均」比較之數，與此人相似，則此人之程度即可視為超越矣。除此之外，關於量度個性，尚有一種需要，即尚須應用明確的方法，求出所謂「集中趨勢」（central tendency）（即測驗法中所稱「平均」mean「中數」median或「眾數」mode）之「可靠性」（reliability）。如所測驗之個性愈有變異，則所測驗之人數當愈多，始能獲得滿意之標準或「平均」。

　　關於量度某種個性之差異程度，已有數法最常用者，茲略述其概要如左：

　　（1）次數分配曲線（frequency curve）　所謂次數分配曲線，例如下圖：平線代表全距離分數，由左向右，起自最低之分數，依次向右，結以最高之分數（此種種分數即由測驗一群兒童某種能力所得之結果）。在平線中每一分數之上，可依得此一級分數人數之多寡，根據所定之單位（如以一人為一單位之類），記一點。俟各點記畢，以一曲線連之，即成所謂次數分配曲線。此圖之功用，在能用圖表示分數之分配大概，由此得覘個性差異之大略情形。如吾人已測驗某人所得之分數，則察視此種曲線，一望而知此人在本群中所居之程度地位。就嚴格言之，此法尚不能稱為明確的量度，惟以其能藉圖畫表明分數分配之大概，用之者頗多，尤以人數在「平均」分數以上或以下者較多時更為有用。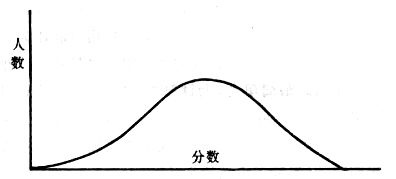

　　職業心理學

　　上圖所示之曲線，乃一種「常態分配」（normal distribution），蓋此圖左右非常均勻也。受測驗之人數愈多，則此種曲線愈近常態。如所得之曲線左右差池不均，稱為「偏態分配」（skewed distribution）。

　　（2）全距離分數（range of scores）　所謂全距離分數，即是從最小分數至數最大分數之距離。有時欲知所測驗之全群成績，僅須敘述全距離分數，即可知其中有無甚大之差異，並可知此群所具之大概程度。核算時，只須從最大分數內減去最小分數。惟此只能作為一種參考之量數，亦非精確之量度也。

　　（3）二十五分差距離（semi-inter-quartile range）　較全距離分數更準確者為二十五分差距離，包含全體分數之中間50％，除去最高分數之四分之一與最低分數之四分之一。此法可表明全群中成績之中間一部分，占全部分之一半。如以Q代二十五分差，其核算之公式如左：

　　

　　公式中之Q1系代表下二十五分點，為一種點數，在此點數以下有全體分數之25％，在此點數以上有全體分數之75％。Q3系代表上二十五分點，亦為一種點數，在此點數以上有全體分數之25％，在此點數以下有全體分數之75％。

　　（4）平均差（average deviation, A. D. , or mean deviation, Mn. D.）　就嚴格言之，上述之三法，其功用只能作為一種參考的量數；若「平均差」則比較的更為明確之量數矣。然平均差尚屬明確量數之最簡單者，乃計算「均方差」（standard deviation）或「機誤」（probable error）之第一步也。所謂平均差，蓋指個人所得之分數與一群中之平均或中數比較之平均差數。其核算方法如左：（差數之正負號不計）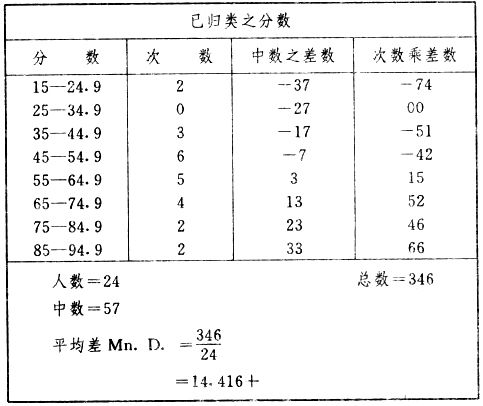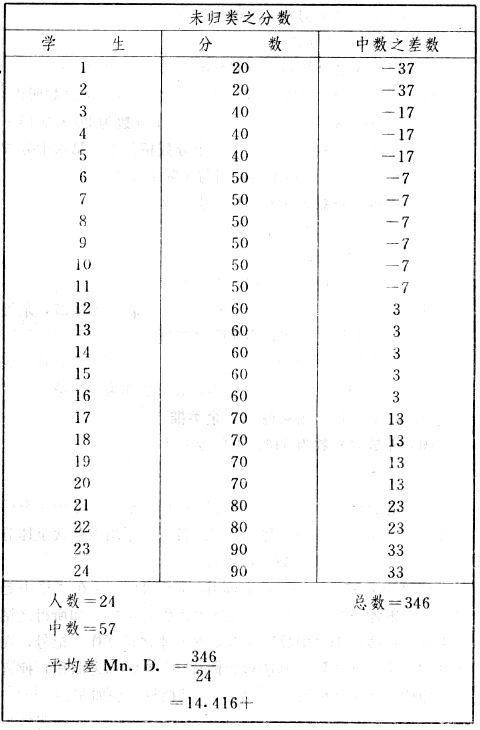

　　職業心理學

　　茲再將上述之平均差算法解釋如左。

　　（甲）未歸類之分數：

　　（a）將原來之分數列成順序分配。（此一步可省）

　　（b）人數＝24，中數為57。（中數系由2除分數總數所得）

　　（c）求各分數與中數之差數。第一個分數為20（為15－24.9之中點）與中數相差37，第三個分數相差17，第六個分數相差7，餘類推。負號可不用，因與實際上無關係。

　　（d）差數之總數為346，正負號不計。

　　（e）平均差等於人數除差數之總數。

　　（乙）已歸類之分數：

　　（a）將原來差數重行排列，求次數分配。

　　（b）第一級15－24.9之離中差為37，第二級為27，餘類推。此差數並非級之差數，乃實際之差數。

　　（c）次數乘差數。例如第一級之次數有2，故用2，乘差數37，總數為74。第二級之次數為零，故總數亦為零。第三級次數為3，差數為17，相乘得51，餘類推。

　　（d）差數之總數為346，正負號不計。

　　（e）平均差＝346／24=14.416+

　　就常態分配言，在「集中趨勢」上下之各一個Q包含全體分數之50％，在「集中趨勢」上下之各一個平均差包含全體分數之57.5％，故後者之數較前者為大。

　　（5）均方差（standard deviation, S. D.）　在「集中趨勢」之上下各一個均方差，約占全體分數之68％。如所得之結果系常態曲線，於「中數」左右依均方差之長度作一記號，在此兩記號上畫兩垂線，則能包含曲線內68.26％之面積，換言之，即能包括全體分數之68.26％。其核算方法如左：

　　職業心理學

　　茲再將上述之均方差算法解釋如左：

　　（甲）未歸類之分數：

　　（a）將原來之分數列成順序分配。（此一步可省）

　　（b）人數＝24，平均數為7.0。因欲免除差數之小數，故用假定的平均數7.5代替平均數7.0。如不用7.5，用9.5或2.5均可。（平均數7.0系用人數除分數總數所得，所以須加.5，因2分實際為2－2.999中點為2.5）。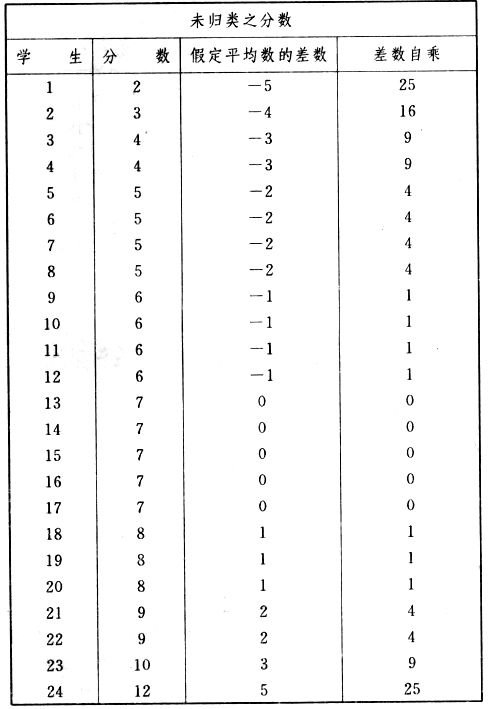

　　職業心理學

　　（c）求各分數與假定的平均數之差數。第一個分數為2，實際為2－2.99，中點為2.5，與假定之平均數相差為5。餘類推。

　　（d）各差數均自乘。

　　（e）差數方之總數為124。

　　（f）均方差S. D. 為人數除差數方之總數，減去校正數的方之方根。校正數的平均數與假定的平均數之差數，在此例內為.5。

　　均方差S.D.= 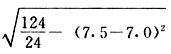職業心理學

　　（乙）已歸類之分數：

　　（a）將原來分數，重行排列，求次數分配。

　　（b）人數＝24，平均數＝7。

　　（c）將接近分配中央任何一級之中點，用為「參照點」。凡用假定的平均數，皆取一級的中點。假定的平均數為7.5。

　　（d）求各級與假定平均數之差數。

　　（e）差數自乘，再乘次數。從上邊乘起：（5）2×1＝25，（4）2×1＝16，（3）2×2＝18。餘類推。

　　（f）均方差S.D.= 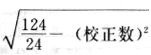職業心理學

平均數與真實的平均數之差數，在此例內為.5。倘遇無差數，則校正數為零。所以須用假定的平均數，再行校正，蓋欲便於核算計，免除小數攙入。

　　（6）機誤（probable error, P. E.）　所謂機誤，亦與分配曲線圖有關係。此指量表上（即分配圖之底線）之一種距離單位；如在「中數」左右，依機誤之距（即長度）作記號，即可表明曲線內全部面積之50％，換言之，即包含全體分數之50％。其算法只須將.6745乘均方差S.D.即得。其公式如左：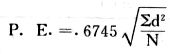

　　職業心理學

　　公式中之d指中數之差數，∑指總數，N指人數。

　　左列一表，表示依據以P. E. 為單位離開「平均」之遠近，其所包含之全體分數中百分之幾亦因之而異。惟此表僅限於常態次數曲線。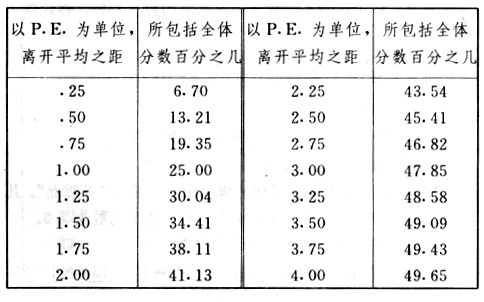

　　職業心理學

　　以上所述可得核算之各種方法，皆以數目字表明在「量表」上與「平均」相離之「距」，藉此表明一級或一群中個性差異之大概趨勢。此數法皆應用統計學於教育方面者也。此外統計學中尚有一法與個性差異之量度亦有重要之關係，即所謂相關度。

　　相關度之創始　相關度創自葛爾頓（Galton），葛爾頓研究遺傳，需要此種量度方法，故此事之探討，由彼開其端焉。關於相關度之進化史與其公式之沿革，其詳情非本章範圍所及。惟「相關係數」（coefficient of correlation）在心理學、教育學、經濟學等等專門科學中皆有甚大之貢獻，尤為研究個性者所不可不知，故其功用與核算方法，為研究職業心理學者所宜特加致意。

　　相關度之意義　所謂相關度，乃一種方法，用以鑒定一組人，或一組學校，或其他團體，其所有之兩種成績間有何連帶關係？如兩種之間有絕對之正比例關係，相關係數（r）為+1.0；如兩種之間僅有反比例之關係，則相關係數為-1.0。如兩種成績彼此間毫無關係，則相關係數為0。據經驗所示，自0至±.4相關為低；自±.4至±.7之相關頗有關係；自±.7至±1.0之相關程度為高者。

　　相關度在教育方面之功用　相關度在教育方面之功用甚大。吾人所採用之智力測驗或教育測驗，其結果是否可恃？教師之評判與測驗之等第是否相符？各種能力彼此間有否連帶關係？各種智力與各種科目彼此間是否有連帶關係？學業成績與實際事業之成功有多大關係？此類問題之答案，皆得以相關度之方法解決之。

　　核算相關度之方法　現今最通行之核算相關度方法，皆用潘阿生（Pearson）所創作之公式：

　　

　　公式中之r指相關係數，∑指總數；x指第一組測驗分數與平均數之差數，y指第二組測驗分數與平均數之差數；N指人數；σx指第一組測驗之均方差，σy指第二組測驗之均方差。上述公式亦可列成如左之公式：

　　

　　茲舉一例如左，說明用此公式核算相關度之方法：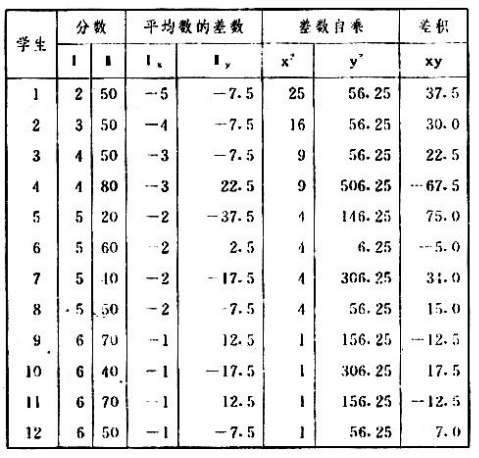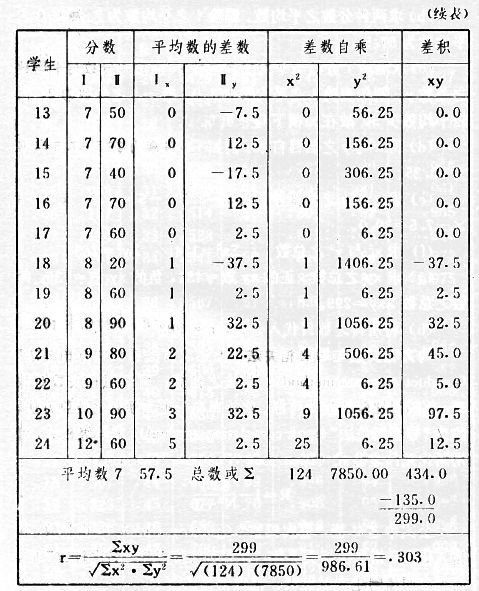

　　職業心理學

　　茲將上表所示相關係數核算法說明如左：

　　（a）依各人之號數，將兩種測驗之分數依次排列，例如第一人所得測驗Ⅰ之分數為2，所得測驗Ⅱ之分數為50。餘類推。

　　（b）求兩種分數之平均數。測驗Ⅰ之平均數為7，測驗Ⅱ之平均數為57.5。

　　（c）求測驗Ⅰ分數與平均數之差數x，測驗Ⅱ分數與平均數之差數y。例如測驗Ⅰ之平均數為7.0，第一人之分數為2，比較平均數少5，故在x項下寫一負5。

　　（d）將x與y之數目自乘。例如-5自乘為25。-7.5自乘為56.25。

　　（e）求x與y之相乘數。例如-7.5×-5＝37.5。又如-4×-7.5＝30.0。

　　（f）求x2與y2之總數　　∑x2＝124　　∑y2＝7850

　　（g）求xy之總數。正的xy數＝434，負的xy數＝135。兩數之總數∑xy＝299。

　　（h）將所得之數目代入公式，r＝.303

　　均方相關法與等級相關法　上述之方法系「均方相關法」（product-moment method），此法之核算，可不用相關數對數表，其結果比較的最為可靠。此外尚有一更為便利之核算方法，稱為「等級相關法」（rank correlation method）。求等級相關，可用斯比亞門之公式（Spearman "Footrule" Formula）：

　　

　　公式中之G指「名次較數」（gains in rank），∑指總數，N指人數，R指名次相關係數。用上列公式得到「名次較數」後，尚須參照潘阿生之對數表，化成相關係數。

　　核算相關度之對數表　化R為r之對數表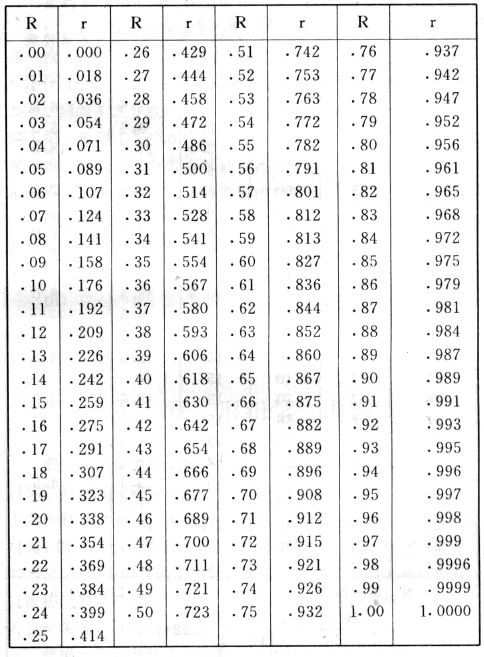

　　

　　既有此表，請再舉一例，以示等級相關之核算法：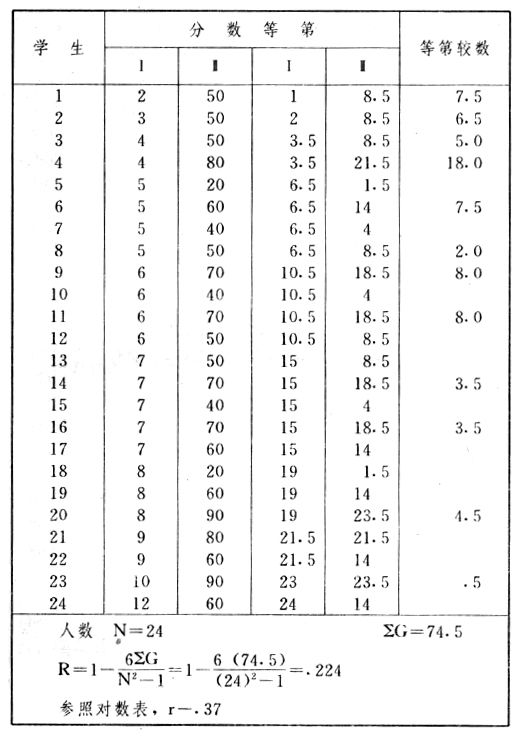

　　職業心理學

　　茲將上述用表核算法說明如左：

　　（a）先將各人之測驗Ⅰ分數，列成比較的等第。例如2分列第一或1；3分列2；4分有兩個，平分3、4等第，故各列3.5；5分有四個，將5、6、7、8四個等第平均之後，各得6.5；餘類推。測驗Ⅱ之分數亦列成等第。例如20分有兩個，平均1、2兩等第，各得1.5；40分有三個，平均3、4、5等第，各得4；餘類推。測驗Ⅰ之分數系以量小者列在最前，如以最大者列在最前亦可，惟兩種測驗之等第須相對照。

　　（b）核算超過第一次等第之數，獲得等第較數。例如8.5-1=7.5；8.5-2=6.5。餘類推。

　　（c）求得等第較數之總數。∑G=74.5

　　（d）代入公式，R=.224，參照對數表化成r，r=.37

學達書庫(xuoda.com)