永樂大典·卷一萬六千三百四十四算

卷一萬六千三百四十四算

　　永樂大典卷之一萬六千三百四十四　十翰

　　算〈演算法十五〉

　　〈少廣九章算經以禦積羃方圓.淳風。按一畆之田。廣一步。長二百四十步。今𣣔截取其從少。以益其廣。故曰少廣術曰。置全步。及分母子。以最下〉

　　〈分母。徧乘諸分子及全步淳風等。按以分母乘全者通其分也。以母乘子者。齊其子也。各以其母除其子置之于左命通分者又以分母徧乘諸分〉

　　〈子。及已通者。皆通而同之。並之為法。淳風等。按諸子悉通。故可並之為法。赤宜用合分術。列數尤多。若用乘則算數至繁。故別置此從省約。置所求〉

　　〈步數。以全步積分乘之為實。置所求步數。以全步積分乘之為實。此以田廣為法。以畆積步為實。置有分者。當同其母。齊其子。以同乘法實。而並齊〉

　　〈於法。今以分母乘全步及子。子如母而一。並以並全法。則法實俱長意亦等也。故其法而一得從步數。實如法而一得從步。嚴恭通原箕法夏侯陽〉

　　〈經雲。田土論文。積土論尺。評重論寸。平方一尺者。積一百寸。立方一尺者。積一千寸也。〉

　　〈九章算經今有田廣一步半求田一畆。問從幾何。答曰。一百六十步。〉

　　〈術曰。下有半。是二分之一。以一為二。半為一。並之得三為法。置田二百四十步亦以一為二乘之為實。實如法得從步。〉

　　〈今有田廣一步半三分步之一。求田一畆。問從幾何。答曰一百三十步。一十一分步之一十。〉

　　〈術曰下有三分以一為六半為三。三分之一為二。並之得一十一為法置田二百四十步亦以一為六乘之為實。實如法得從步。〉

　　〈今有田廣一步半三分步之一四分步之一。求田一畆。問從幾何。答曰一百一十五步五分步之一。〉

　　〈術曰下有四分以一為一十二半為六三分之一為四。四分之。一為三。並之得二十五以為法置田二百四十步。亦以一為一十二乘之為實。〉

　　〈實如法而一得從步今有田廣一步半三分步之一四分步之一五分步之一。求田一畆。問從幾何。〉

　　〈答曰一百五步一百三十七分步之一十五。術曰。下有五分以一為六十半為三十。三分之一為二十四分之一為〉

　　〈一十五。五分之一為一十二並之得一百三十七以為法。置田二百四十步。亦以一為六十乘之為實實如法得從步〉

　　〈今有田廣一步半三分步之一四分步之一五分步之一。六分步之一。求田一畒問從幾何〉

　　〈答曰九十七步四十九分步之四十七術曰下有六分以一為一百二十半為六十三分之一為四十。四分之〉

　　〈一為三十五分之一為二十四六分之一為二十.並之得二百九十四以為法。置田二百四十步亦一為一百二十乘之為實。實如法得從。〉

　　〈楊輝詳解今有田一畆廣一步半全步乃一分之一。半步是二分步之一。三分步之一。四分步之一五分步之一六分步之一問從數。〉

　　〈答曰。九十七步四十九分步之四十七解題此問田一畒為主以廣求從但其中加分母分子。位次頗多。若用〉

　　〈合分互乘之法豈不繁劇古人棄合分之術。而以諸母自乘為全步之積分乘子。卻以諸。母各除其子取其本積。並之為廣而求問。特設少廣〉

　　〈之問。法曰。列置全步。及分母子。而副置分母自乘。分母自乘。是求全步之積分也。以乘全步及子。各以本母除之。並之為法。齊子之意。以代互〉

　　〈乘。以全步積分乘畆步為實。法既通分。實亦合一體通分。實如法而一。為法除實也。少廣。李淳風等曰。一畆之田。廣一步。長二百四十步。今〉

　　〈截從少以益廣故曰少廣。古術曰。置全步。及分母子。以最下分母遍乘諸分子及全步淳風等。以分母乘全步者。通其分也。以母乘其子者。齊〉

　　〈其子也各以其母除其子。置之于左命通分者。又以母遍乘諸分子。及已通者皆通而同之並之為法淳風等諸子悉通。故可並之為法。亦以〉

　　〈宜用合分術列數尤多。若用乘則算數置繁。故別置此術從省約。置所求步數以全步積分乘之為實置所求步數以全步積分乘之為實。此〉

　　〈以田廣為法一畆積步為實法有分者。當共其母。齊其子。以同乘法實。而並齊於法今以分母乘全步及子子如母而一併以並全法則實供〉

　　〈長意亦等也故如母而一實如法而一得從。按古草曰。本是三叚。古人文言之置全步及分母子一步二分之一三分之一。四分之一。五〉

　　〈分之一六分之一以最下分母六遍乘諸分子及全步六位各六。各以其母分母除其子置之于左全步得六二分之一得三三分之一得二。〉

　　〈四分之一得一餘四分之二五分之一得一餘五分之一六分之一得一命通分者用母除子則分子之內又有分子矣又以母遍乘諸分子。〉

　　〈已通者皆通而同之。母即分子之母。當以四分與五分遍乘諸子。內其全步。得一百二十其二分之一得六十其三分之一得四十。其四分之〉

　　〈一得三十其五分之一得二十四。其六分之一得二十。並之為法並得二百九十四。置所求步數二百四十。以全步積分一百二十乘之為實。〉

　　〈二萬八千八百。此是第一呌。合雲實如法而一。法有分者。當同其母。齊其子。欠諸分母三字。以同乘法實。而並齊於法。下文合雲。實如法而〉

　　〈一。宜以田廣一步。二分步之一。三分步之一。求田一畆四步。三分步之一。問從為題。即法有分者當同其母。齊其子之句。先以母二分。次以三〉

　　〈分。並乘全步及子三位各得六。以各母除子。並得十一。法雲以同乘法實者。謂法實皆有分子。用諸母同乘其實。一畆四步。三分步之一。以分〉

　　〈母通為七百三十三。以分母六乘得四千三百九十八。仍以實母三同乘法得三十三。是並齊於法。下文便當雲實如法而一。除得一百三十〉

　　〈三步。十一分步之三。以分母欠自乘而三字乘全步。及子。子如欠各母而一。欠並之為法。實如法而一得從。後草所編之術。草曰。列置全〉

　　〈步。及分母子。全步。即一分之一。以分母一。二。三。四。五。六。列右行。分子之一。一。一。一。一。一。列左行。而副置分母自乘。不動正位。別置分母自乘。得〉

　　〈七百二十。以乘全步及分子。全步得七百二十。分子皆為七百二十。各以本母除子。全步得七百二十。其二分之一得三百六十。其三分之一〉

　　〈得二百四十。其四分之一得一百八十。其五分之一得一百四十四。其六分之一得一百二十。並之得一千七百六十四。為法。以全步積分通〉

　　〈畆步。通二百四十步。為一十七萬二千八百分。為實。實如法而一。以一千七百六十四分為法除實。得九十七步。餘一千六百九十二。約之得〉

　　〈四十九分步之四十七九章算經今有田廣一步半三分步之一。四分步之一。五分步之一。六分〉

　　〈步之一。七分步之一。求田一畆問從幾何。答曰九十二步一百二十一分步之六十八。〉

　　〈術曰。下有七分以一為四百二十半為二百一十三分之一為一百四十。四分之一為一百五五分之一為八十四六分之一為七十七分之〉

　　〈一為六十並之得一千八十九以為法。置田二百四十步。亦以一為四百二十乘之為實。實如法得從步。〉

　　〈今有田廣一步半三分步之一四分步之一。五分步之一六分步之一。七分步之一。八分步之一求田一畆問從幾何。〉

　　〈答曰八十八步七百六十一分步之二百三十二術曰下有八分。以一為八百四十半為四百二十。三分之一為二百八〉

　　〈十。四分之一為二百一十。五分之一為一百六十。八六分之一為一百四十七分之一為一百二十八分之一為一百五。並之得二千二百八〉

　　〈十三以為法置田二百四十步亦以一為八百四十乘之為實。實如法得從步〉

　　〈今有田廣一步半三分步之一。四分步之一五分步之一。六分步之一。七分步之一。八分步之一九分步之一求田一畆問從幾何〉

　　〈答曰八十四步。七千一百二十九分步之五千九百六十四。術曰。下有九分。以一為二千五百二十。半為一千二百六十。三分之一〉

　　〈為八百四十。四分之一為六百三十。五分之一為五百四。六分之一為四百二十。七分之一為三百六十八分之一為三百一十五。九分之一〉

　　〈為二百八十。並之得七千一百二十九以為法。置田二百四十步。亦以一為二千五百二十乘之為實。實如法得從步。〉

　　〈今有田廣一步半。三分步之一。四分步之一。五分步之一。六分步之一。七分步之一。八分步之一。九分步之一。十分步之一。求田一畆。問從幾何。〉

　　〈答曰。八十一步。七千三百八十一分。步之六千九百三十九。術曰。下有一十分。以一為二千五百二十。半為一千二百六十。三分之〉

　　〈一為八百四十。四分之一為六百三十。五分之一為五百四。六分之一為四百二十七分之一為三百六十。八分之一為三百一十五。九分之〉

　　〈一為二百八十。十分之一為二百五十二。並之得七千三百入十一以為法。置田二百四十步。亦以一為二千五百二十乘之為實。實如法得〉

　　〈從步。今有田廣一步半三分步之一。四分步之一。五分步之一。六分步之一。七〉

　　〈分步之一。八分步之一。九分步之一。十分步之一。十一分步之一。求田一畆。問從幾何。〉

　　〈答曰。七十九步。八萬三千七百一十一分。步之三萬九千六百三十一。術曰。下有一十一分。以一為二萬七千七百二十。半為一萬三千八百〉

　　〈六十。三分之一為九千二百四十。四分之一為六千九百三十。五分之一為五千五百四十四六分之一為四千六百二十。七分之一為三千〉

　　〈九百六十。八分之一為三千四百六十五。九分之一為三千八十一。十分之一為二千七百七十二十一分之一為二千五百二十。並之得八〉

　　〈萬三千七百一十一以為法置田二百四十步。亦以一為二萬七千七百二十乘之為實。實如法得從步〉

　　〈今有田廣一步半三分步之一。四分步之一。五分步之一。六分步之一。七分步之一。八分步之一九分步之一。十分步之一。十一分步之一。十二分〉

　　〈步之一求田一畆問從幾何。答曰。七十七步。八萬六千二十一分。步之二萬九千一百八十三。〉

　　〈術曰。下有一十二分。以一為八萬三千一百六十。半為四萬一千五百八十三分之一為二萬七千七百二十四分之一為二萬七百九十。五〉

　　〈分之一為一萬六千六百三十二。六分之一為一萬三千入百六十。七分之一為一萬一千八百八十。八分之一為一萬三百九十五。九分之〉

　　〈一為九千二百四十一。十分之一為八千三百一十六。十一分之一為七千五百六十。十二分之一為六千九百三十。並之得二十五萬八千〉

　　〈六十三以為法。置田二百四十步。亦以一為八萬三千一百六十乘之為實實如法得從步。淳風等。按凡為術之意。約省為善。宜雲下有一十〉

　　〈二分。以一為二萬七千七百二十。半為一萬三千八百六十。三分之一為九千二百四十。四分之一為六千九百三十。五分之一為五千五百〉

　　〈四十四。六分之一為四千六百二十。七分之一為三千九百六十。八分之一為三千四百六十五。九分之一為三千八十。十分之一為二千七〉

　　〈百七十二。十一分之一為二千五百二十。十二分之一為二千三百一十。並之得八萬六千二十一以為法。置田二百四十步。亦以一為二萬〉

　　〈七千七百二十乘之以為實。實如法得從步。其術亦得知不繁也。開方楊輝摘奇演算法校正辯古通源。開方不盡之法。開方除不盡之數命〉

　　〈為分子術曰。倍隅數入廉一退。平方二因。立方三因。併入下法一算。緫為分母。以命分子之數。再求積數還源術曰。置方面全步。以分母通之。並〉

　　〈入分子。自乘於頭。又以分子減分母余以分子乘之得數。併入頭位為實。商除還原。無此一叚。以分母自乘為法。實如法而一平方本積有分子。〉

　　〈即是原方面有之分術曰。分母乘全步。併入分子。開方除得方面散分積數。別置原分母。開方除得方面分母。以除前叚散積乃得方面幾步幾分〉

　　〈之幾楊輝詳解開方作法本源。出釋鎮算書。賈憲用此術。〉

　　〔插圖〕

　　〈左袤乃積右袤乃隅算。〉

　　〈中蔵者皆廉。以廉乘商方。〉

　　〈命實而除之。〉

　　〈增乘方求廉法草曰。釋鎮求廉本源。列所開方數。如前五乘方。列五位隅算在外。以隅算一。自下增入前位。至首位而止。首位得六。第二位得〉

　　〈五。第三位得四。第四位得三。下一位得二。複以隅算如前升增。逓低一位求之。〉

　　〈求第二位六舊數五加士而止四加六為士三加三為六二加一為三〉

　　〈求第三位六十五並舊數十加十而止六加四為十三加一為四〉

　　〈求第四位〉

　　〈六十五二十並舊數十加五而止四加一為五求第五位〉

　　〈六十五二十十五並舊五加一為六上㢘二㢘三㢘四㢘下㢘〉

　　〈楊輝纂類賈憲立成釋鎻平方法曰。置積為實別置一算名曰下法。于實數之下自末位常超一位。約實至首位盡而止。實上商至第一位得〉

　　〈數下法之上。亦置上商。名曰方法命上商除實。二乘方法。一退為廉。下法再退于上商之次續商第二位得數扵廉法之次。照上商置隅。以方〉

　　〈廉二法皆命上商除實二乘隅法併入廉法一退。下法再退商置第三位得數下法之上照上商置隅以廉隅二法皆命上商除實盡。得平方〉

　　〈一面之數積有分子者以分母乘其全入內子又以分母再二次自乘乘之積圓者。以國法十二乘之。開平方求積。如分母自乘而一。增乘〉

　　〈開平方法曰。第一位上商得數以乘下法為平方命上商除實。上商得數以乘下法入平方一退為廉第二位再商得數。以乘下法為隅。命〉

　　〈上商除實訖以上商得數乘下法入隅皆名曰廉一退下法再退以求第三位商數第三位如第二位用法求之〉

　　〈賈通全能集開方以積使商除除得其間上置諸下另倍為方法數卻將方倍減其餘得其次數上商續方下旁邉也續歟上下再將續除積。積之〉

　　〈數儘自昭如若還不盡倍方次逐一將方位數除除見數來商又續。只將此續取空虛〉

　　〈開方之法有三有平方。有直方有立方其法最難取算。然公私亦少用之但平方一法間自用之收算。方田一面。不可不載一法於其間也。〉

　　〈丁巨演算法方求圓。二十二乘七除圓求方。七乘二十二除。平面求周。圓十二乘方四乘外圓求積圓物六乘十二除。方物。八乘十六除。立圓求徑。〉

　　〈九乘十六除立方求圓十六乘九除見斜求方。五乘。七除見方求斜。七乘。五除。〉

　　〈九章算經今有積五萬五千二百二十五步。問為方幾何答曰二百三十五步。〉

　　〈今有積二萬五千二百八十一步。問為方幾何。答曰。一百五十九步〉

　　〈今有積七萬一千八百二十四步。問為方幾何。答曰。二百六十八步。〉

　　〈楊輝詳觧解題圜三象天。方四象地。圜居方四分之三。以積立術。求方助乘除之妙用。考究源流。莫不由此。法曰。置積為實。別置一算名曰下〉

　　〈法。原下之法。於實數之下。自末位常超一位。初乘時過一位。今超一位。約實至首位盡而止。一下定一。一百下定十。萬下定百。百萬下定千。於〉

　　〈實上商置第一位得數。以方法一一。二二。三三四四。五五。六六。七七。八八九九。之數為商。商本體實數。下法之上。亦置上商數。即原乘法數也〉

　　〈名曰方法。於本積內。去其一方。命上商除實。法實相呼。以破積數。二乘方法。一退為廉。一方帶兩直。以助其狀如廉。故二乘退位。下法再退。下〉

　　〈法即定位之算。再退復位。于上商之次。續商第二位得數。與上意同。于廉。法之次。照上商置隅。一方帶二廉。正闕一角。角即名隅。以方廉二法。〉

　　〈亦原乘之法也。皆命上商除實。二乘隅法併入廉法一退。倍隅人廉作一大方。以求次位得數。下法再退。前意商置第三位得數。下法之上。照〉

　　〈上商置隅。以廉隅二法。皆命上商除實。第二位解意同。得平方一面之數。更有不盡之數。依第三位體面倍隅入廉。退位商之。草曰。置積為〉

　　〈實。七萬一千八百二十四步。別置一算為下法。原下之法。從末常超一位約實。百下約十。萬下約百。實上商置第一位得數二百。下法之上。亦〉

　　〈置上商二百名曰方法二百乃命上商除實。四萬余三萬一千八百二十四。二乘方法得四百步一退為廉四百下法再退。百下約十。扵上商〉

　　〈之次續商第二位得數六十。共為二百六十。廉法之次。照上商置隅六十以廉隅二法皆命上商除實二萬七千六百。餘四千二百二十四。二〉

　　〈乘隅法並于廉。得五百二十。一退五百二十。下法再退。於末位下定一。又于上商置第三位得數二百六十之次。商置八。下法之上亦置八為〉

　　〈隅除實適盡合問〉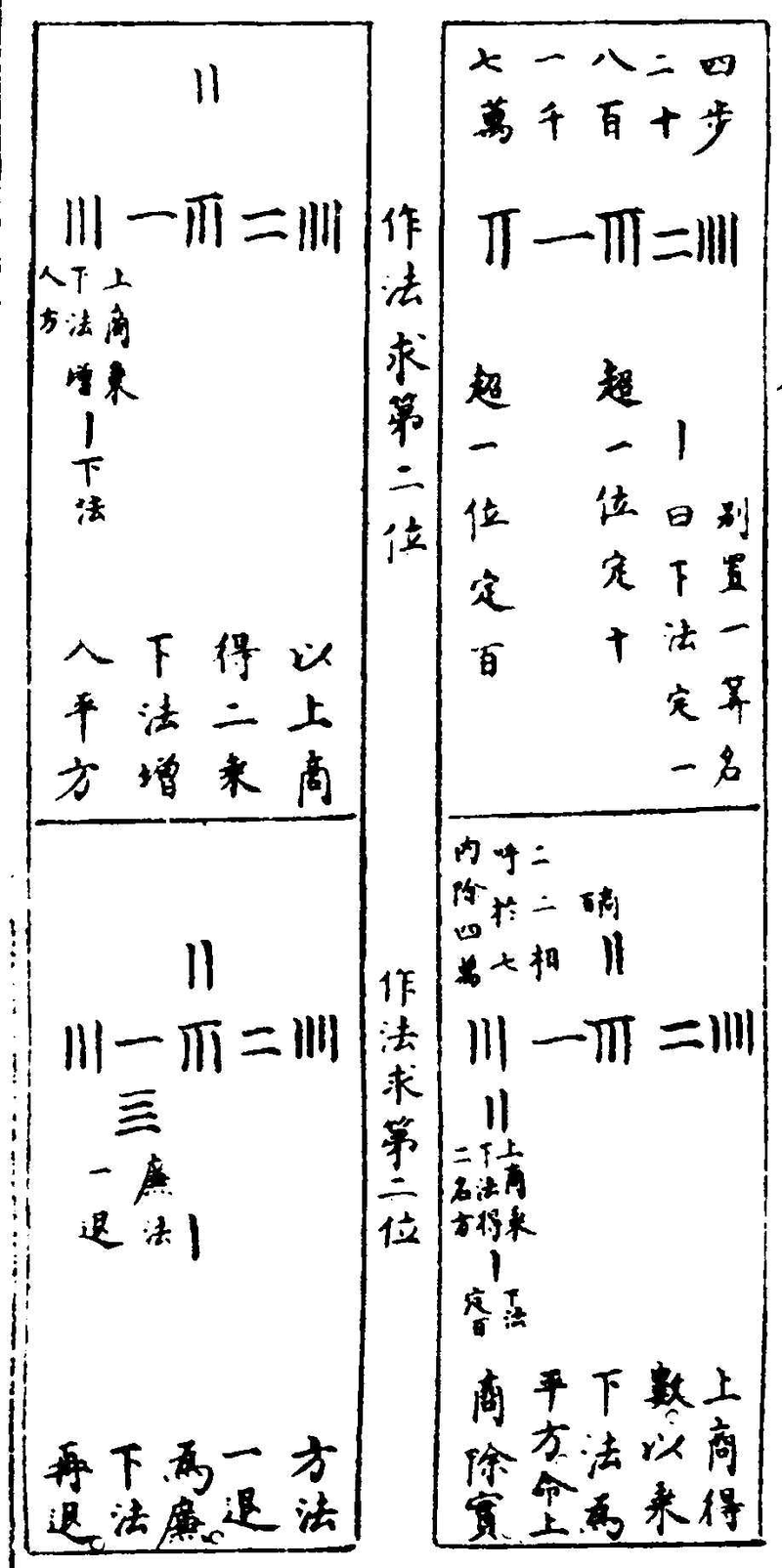

　　〔插圖〕

　　〈增乘開平方法。以商數乘下法。逓增求之。商第一位。上商得數以乘下法為乘方。命上商除實。上商得數以乘下法入乘方。一退為廉。下法〉

　　〈再退。商第二位。商得數以乘下法為隅。命上商除實訖。以上商得數乘下法入隅皆名曰廉。一退。下法再退以求第三位商數。商第三位。〉

　　〈用法如第二位求之　增乘開平方圖。以圖參法。取用可知。〉

　　〈布位定位商第一位〉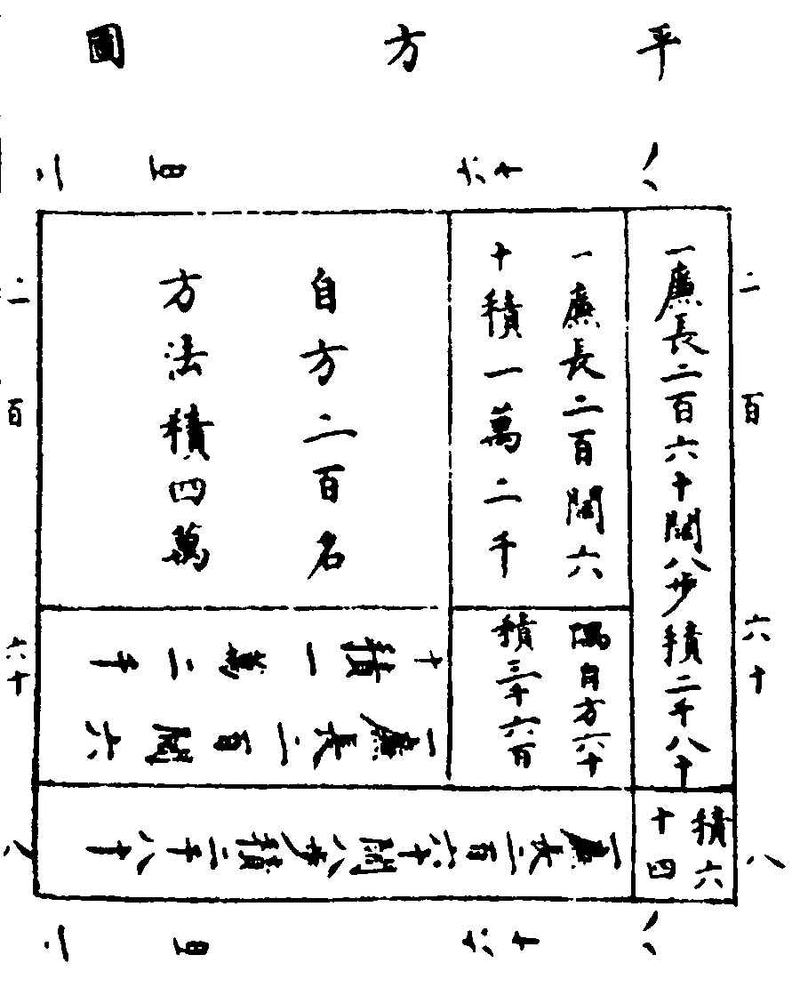

　　〔插圖〕

　　〈商第二位作法求第三位〉

　　〔插圖〕

　　〈嚴恭通原算法術曰。置積為實。借一算步之超一等。言百之面十也。言萬之面百也。上商二百乘下隅為廉。二百呼除本積二二除去四萬。餘積〉

　　〈三萬一千八百二十四步為實。倍廉為方法得四百。續上商六十乘下隅為廉六十。于四百之下與上商六十呼除本積。四六除去二萬四千。〉

　　〈六六除去三千六百。餘積四千二百二十四步為實。又倍廉六十得一百二十併入方法共五百二十。續上商八步乘下隅為廉八步。於五百〉

　　〈二十之下與上商八步呼除本積。五八除去四千。二八除去一百六十。八八除去六十四步適畫。得方面二百六十八步合前問。〉

　　〈九章算經又有積五十六萬四千七百五十二步。四分步之一。問為方幾何。答曰。七百五十一步半。〉

　　〈嚴恭通原算法術曰。列積步以四分通之納子。又以四分再自乘得六十四乘之為實。以開方法除之得一萬二千二十四分。卻以四分自乘〉

　　〈之。得一十六為法除之即得。今有積三十九億七千二百一十五萬六百二十五步。問為方幾何〉

　　〈答曰。六萬三千二十五步開方求方羃之一面也術曰置積為實借一算步之超一等。言百之面〉

　　〈十也。言萬之面百也。議所得以一乘所借一算為法而以除。先得黃甲之面。上下相命是自乘而除也除已倍法為定法。倍之者豫張面面朱〉

　　〈羃定袤以待複除。故曰定法其複除折法而下欲除朱羃者本當副置所得乘方倍之為定法以折議乘而以除。如是當複步之而止乃得相〉

　　〈命故使就上折下複置借算步之如初以覆議一乘之欲除朱羃之甫黃乙之羃。其意如初之所得也所得副以加定法以除以所得副從定〉

　　〈法。再以黃乙之面加定法者是則張兩青羃之袤複除折下如前。若開之不盡者為不可開當以面命之術或有以借箕加定法而命分者。雖〉

　　〈粗相近不可用也。凡開積為方方之自乘當還複有積分令不加借算而命分則常微少其加借算而命分則又微多其數不可得而定故惟〉

　　〈以面命之為不失耳譬猶以三除十以其餘為三分之一而複其數可以舉。不以面命之加定法如前求其微數微數無名者以為分子。其一〉

　　〈退以十為母其再退以百為母退之彌十其分彌細。則朱羃雖有所乘之數不足言之也若實有分者通分內子為定實。乃開之訖開其母報〉

　　〈除。淳風等。按分母可開者並通之積先合二母。既開之後一母尚存。故開分母求一母為法以報除也。若母不可開者又以母再乘定實乃開〉

　　〈之訖。令如母而一。淳風等。按分母不可開者本一母也。又以母乘之乃合二母既開之後亦一母存焉。故令一母而一得全面也又按此術開〉

　　〈方者。求方羃之面也。借一算者假借一算空有列位之名而無除積之實。方隅得面。是故借算列之于下步之超一等者。方十自乘其積有百〉

　　〈方百自乘其積有萬。故超位至百而言十。至萬而言百。議所得以一乘所借算為法而以除者先得黃甲之面。以方為積者兩相乘故開方除〉

　　〈之還令兩面。上下相命是自乘而除之。除已倍法為定法者。實積未盡當複更除。故豫張兩面朱羃袤以待複除。故曰定法。其複除折法而下〉

　　〈者欲除朱羃。本當副置所得成方倍之為定法。以折議乘之而以除如初。是當複步之而止乃得相命故使就上折之而下複置借算步之如〉

　　〈初以覆議一乘之所得。副以加定法。以定法除者。欲除朱羃之角。黃乙之羃以所得副從定法者再以黃乙之羃加定法。是則張兩青羃之袤。〉

　　〈故如前開之即合所問孫子算經今有積二十三萬四千五百六十七步。問為方幾何。〉

　　〈答曰四百八十四步。九百六十八分步之三百一十一術曰置積二十三萬四千五百六十七步為實次借一算為下法。步之〉

　　〈超一位至百而止。商置四百於實之上副置四萬。於實之下。下法之上名為方法命上商四百除實除訖。倍方法一退。下法再退。複置上商八〉

　　〈十以次前商副置八百於方法之下下法之上名為廉法。方廉各命上商八十以除訖倍廉法上從方法一退方法下法再退複置上商四以〉

　　〈次前副置四於方法之下。下法之上名曰隅法方廉隅各命上商四除實除訖上商得四百八十四。下法得九百六十八。不盡三百一十一。是〉

　　〈為方四百八十四步九百六十八分步之三百一十一。夏候陽算經今有田二十一頃七十八畆一百八十步。問為方幾何。〉

　　〈答曰七百二十三步奇百七十一步。術曰先置頃畒扵上以二百四十步乘之得五十二萬二千七百二十〉

　　〈步內零一百八十步以開方除之。借一算為下法步之超一位至百止。萬上置上商七百。下亦置七萬於實位之下。下法之上。命上商除實訖〉

　　〈倍方為一十四萬。方法一退。下法再退。又置上商二十于前商後又置二百扵方法之下。下法之上。名曰隅法。以方隅二法皆命上商以除實〉

　　〈訖。倍隅法為四百從上。方法一退。下法再退。又置上商三于前商二十之後又置三步於方法之下。下法之上。名曰隅法。以方隅二法皆命上〉

　　〈商除實訖倍隅法得六從上。方法得一千四百四十六。即是上方得七百二十三步奇一百七十一步。〉

　　〈五經算術論語千乘之國法。子曰道千乘之國。注雲。司馬法六尺為步。步百為畆畆百為夫夫三為屋。屋三為井。井十為通。通十為成。成出革車〉

　　〈一乘然千乘之賦其地千乘也。今有千乘之國。其地千成。計積九十億步問為方幾何〉

　　〈答曰。三百一十六裡六十八步。一十八萬九千七百三十七。分步之六萬二千五百七十六。〉

　　〈術曰。置積步為實。開方除之即得。按千乘之國。其地千成。方十裡。置一城地十裡。以三百步乘之得三千步。重張相乘得九百萬步。又以千成〉

　　〈乘之得積九十億步。以開方除之。即得方數也。開方法曰。借一算為下法。步之常超一位至萬而止。置上商九萬於實之上。又置九億於實之下。〉

　　〈下法之上名曰方法。命上商九萬以除實畢。倍方法九億得十八億乃折之方法一折。下法再折又置上商四千於上。以次前商之後。又置四〉

　　〈百萬於方法之下下法之上名曰隅法。方隅皆命上商四千以除實畢。倍隅法得八百萬上從方法得一億八千八百萬乃折之方法一折。下〉

　　〈法再折又置上商八百於上。以次前商之後又置八萬於方法之下。下法之上名曰隅法。方隅皆命上商八百以除實畢。倍隅法得十六萬上〉

　　〈從方法得一千八百九十六萬乃折之方法一折。下法再折又置上商六十於上以次前商之後。又置六百於方法之下。下法之上名曰隅法〉

　　〈方隅皆命上商六十以除實畢。倍隅法得一千二百上從方法得一百八十九萬七千二百乃折之。方法一折。下法再折又置上商八於上以〉

　　〈次前商之後又置八扵方法之下下法之上名曰隅法方隅皆命上商八以除實畢倍隅法得一十六上從方法下法一亦從之得一十八萬〉

　　〈九千七百三十七分步之六萬二千五百七十六以裡法三百步除之得三百一十六裡不盡六十八步即得方三百一十六裡六十八步一〉

　　〈十八萬九千七百三十七分步之六萬二千五百七十六也楊輝摘奇演算法積一千三百尺。問平方一面幾尺。〉

　　〈答曰。三十六尺七十三分尺之四開方草曰。置積為實。一千三百。別置下法一算從常超一位約實。百下〉

　　〈定十。上商方面三十以乘下法為方法三十命上商除實九百。餘實四百。以二因方法。一退為廉六十下法再退定零上又商第二位方面六〉

　　〈尺。以乘下法為隅六尺。以廉隅二法六十六尺命上商除實三百九十六尺餘實四尺即開方不盡之數。二因隅法併入廉法。共七十二添入〉

　　〈下法一算共七十三。命為分母。所餘四尺。命為分子合問還源求原積草曰。置方面三十六尺。七十三分尺之四。以分母通全尺併入分子〉

　　〈共二千六百三十二自乘於上。得六百九十二萬七千四百二十四。別置分子減分母余分子四減分母七十三餘六十九以乘分子。六十九〉

　　〈乘子四。得二百七十六。並之為實。得六百九十二萬七千七百。以分母自乘為法。得五千三百二十九。以法除之。得原積一千三百尺。〉

　　〈今有積一千五百九十尺。六十四分尺之一。問平方面幾何。答曰。三十九尺。八分尺之七。〉

　　〈原積有分子開平立術曰。以分母六十四。通積尺一千五百九十。分子一併之為實。一十萬一千七百六十一。開平方得方面分子積數三百〉

　　〈一十九置原分母開方六十四。開平方得八。為方面分母。以除方面分積三百一十九。得方面尺數三十九尺。餘八分尺之七。〉

　　〈透簾細草今有平方積五萬五千六百九十六尺。問一面方多少。答曰。二百三十六尺。〉

　　〈法曰平立開之草曰。置積為實。借一運算元為約法。常超一位。進二度合商百。乃上商二百尺。二因常隅。又名下法。又名約法。得二萬為方法。〉

　　〈命商除實四萬了。倍方法一退得四十。約法二退於百之下。續商三百尺。三因隅法得三百尺。併入立法得四千三百。命商三十除實。餘有二〉

　　〈千七百九十六在方法內又添隅法三百一退得四百六十。隅法二退為二尺上續商六尺。又於方法內添隅法六尺一步。得四百六十六尺。〉

　　〈乃命商六尺除實恰盡丁巨算法術曰置積在地商二二如四除了四萬另於上退二位置二合商百並於下置二為方倍之得四將四問得〉

　　〈四三一十二又除一萬。二千于上續商三下方亦續三又將上下三為三三如九又除九百實有二千七百九十六又將立三倍為六共得四〉

　　〈六卻以四商得四六二十四又除二千四百。續商六以六除盡。丁巨演算法今有平方積六十二萬二千五百二十一尺問一面幾何。〉

　　〈答曰七百八十九尺置積尺以一算於一尺之下為隅常超一位至二萬尺之下上商七呼〉

　　〈一七生方七。即扵隅法之上布七作方法。呼七七四十九去積四十九萬尺。倍方法為一十四方法一退隅法二退上商八呼一八生方八。於〉

　　〈方法之後對上商八之下布方法八呼一八如八去積八萬尺。余積五萬二千五百二十一尺呼四八三十二去積三萬二千尺又呼八八六〉

　　〈十四去積六千四百尺倍方法八得方法一百五十六。方法一退。隅法二退上商九呼一九生方九即於生法之後對上商九之。下布方法九〉

　　〈呼一九如九去積九千尺。呼五九四十五去積四千五百尺。呼六九五十四去積五百四十尺。九九八十一去積八十一尺適盡。此平方之法〉

　　〈頗難通。故複二例。若有積九千六百零四尺。開平方一面幾何。然九十八尺。置積在地如上除也。〉

　　〈賈通全能集今有方田六畆零四步。問一方面該步幾何。答曰。該方三十八步。〉

　　〈法曰。置畆為步。答入零步。開平方除之合問。開平本法。置緫法在地用商三三如九。另於上退二位置三合商十。下亦另置三為方法在地〉

　　〈止有五百四十四。卻以方法三倍之得六。又以六商除六八四十八。續上商八在地。止有六十四方下亦置八。以八八呼除六十四恰盡。商得〉

　　〈三十八步為一方面。其餘開方皆仿此。嚴恭通原演算法今有積八萬步問為方若干。〉

　　〈答曰二百八十二步。五百六十五分之四百七十六。術曰置積為實。借一算步之超一等上商二百乘下隅為廉。二百呼除〉

　　〈本積二二除去四萬余積四萬步為實。倍廉為方法得四百。續上商八十乘下隅為廉八十。于四百之下與上商八十呼除本積四八除去三〉

　　〈萬二千。八八除去六千四百。余積一千六百步為實。又倍廉八十得一百六十。併入方法共五百六十續上商二步。乘下隅為廉二步。扵五百〉

　　〈六十之下與商二步呼除本積二五除去一千二六除去一百二十。二二除去四步。余積四百七十六步又倍廉二步得四併入方法並借一〉

　　〈隅算共得五百六十五是得方面二百八十二步五百六十五分之四百七十六合前問。〉

　　〈今有積一百二十一步問為方若干答曰。一十一步。〉

　　〈今有積三百六十一步。問為方若干。答曰。一十九步。〉

　　〈今有積七百步。問為方若干。答曰。二十六步。五十三分步之二十四。〉

　　〈今有積一千步。問為方若干。答曰。三十一步六十三分步之春十九。〉

　　〈術曰。俱以前開方除之即得。九章算經今有積一千五百一十八步。四分步之三。問為圓周幾何。〉

　　〈答曰。一百三十五步。於徽術。當週一百三十八步。一十分步之一。淳風算。按此依宻平。為週一百三十八步。五十分步之九。〉

　　〈楊輝詳解解題以方改圓驗方圓相通也。圓居四分之三。法曰。分母乘全步入內。子以圓法十二乘之。又以分母再自乘乘之。開平方求積。以〉

　　〈分母自乘為法除之。以分母自乘為法除實得周。草曰。分母四。乘全步一千五百一十八步。入內子三。得六千七十五。以圓法十二乘之。得〉

　　〈七萬二千九百。又以分母四。再自乘為六十四。乘之為實。四百六十六萬五千六百。開平方別置一算為下法。原下之法。從末常超一位約實〉

　　〈百下約十。萬下約百百萬下約千。實上商置第一位得數二千。下法之上。亦置上商二千。名曰方法。乃命上商除實四百萬。二乘方法一退為〉

　　〈廉。乘作四千退為四十。下法再退。百下定十。于上商之次續商第二位得數一百。共為二千一百。廉法之次。上商置隅一百。以廉隅二法皆命〉

　　〈上商除實。除四十一萬。余二十五萬五千六百。二乘隅法並為廉一退。得四千二百。下法再退。扵末位百下定十。又以上商置第三位得數六〉

　　〈十。下法之上亦置隅六十。除實適盡得二千一百六十。以分母自乘為法除之。嚴恭通原算法術曰。列積步。以四分通之納子十二乘之。又以〉

　　〈四分再自乘得六十四。乘之為實。以開方除之。得二千一百六十分。卻以四分自乘得一十六。為法除之即得。〉

　　〈今有積三百步問為圓周幾何。答曰六十步於微術。當週六十一步。五十分步之十九淳風等。按〉

　　〈依宻率。為週六十一步一百分步之四十一。術曰。置積步數。以十二乘之。以開方除之即得周。此術以週三徑一為〉

　　〈率。與舊圓田術相返覆也。於微術以三百一十四乘積。如二十五而一。所得開方除之即周也。開方除之即徑是為據見羃以求周猶失之扵〉

　　〈微少。其以二百乘積一百五十七而一。開方除之即徑。猶失之扵微多。淳風等。按此注於徽術求周之法。其中不用開方除之即徑六字。今〉

　　〈本有者衍剩也。依宻率八十八乘之七而一。按週三徑一之率。假今週六徑二。半周半徑相乘得羃三。週六自乘得三十六。俱以等數除羃得〉

　　〈一周之數十二也。其積本周自乘。合以一乘之。十二而一得積三也。術為一乘不長。故以十二而一得。此積。今還原。置此積三以十二乘之者〉

　　〈複其本周自乘之數。凡物自乘開方除之複其本數。故開方除之即周。孫子算經今有積三萬五千步。問為圓幾何。〉

　　〈答曰。六百四十八步。一千二百九十七分步之九十六。術曰。置積三萬五千步。以一十二乘之得四十二萬為實。次借一算為〉

　　〈下法。步之超一位至百而止。上商置六百。余於實之上副置六萬。於實之下。下法之上。名為方法。命上商六百除實。除訖倍方法。方法一退。下〉

　　〈法再退複置上商四十。以次前商副置四百於方法之下。下法之上。名為廉法方廉各命上商以除實除訖。倍廉法從方法。方法一退。下法再〉

　　〈退。複置上商八次前商。副置八於方法之下下法之上名為隅法。方廉隅各命上商八以除實除訖倍隅法從方法。上商六百四十八。下法得〉

　　〈一千二百九十七不盡九十六是為方六百四十八步一千二百九十七分步之九十六〉

　　〈嚴恭通原演算法今有積一千二百步欲為圓問徑若干答曰四十步〉

　　〈術曰列積步以四乘三除得一千六百步以開方除之即得五徑算術禮記投壺法。壺頸修七寸。腹修五寸。口徑二寸半容鬥五升注〉

　　〈雲修長也。腹容鬥五升三分益一則為二鬥得圓囷之象積三百二十四寸。以腹修五寸約之所得求其圓周二尺七寸有奇是為腹徑九寸有餘〉

　　〈甄鸞按斛法一尺六寸二分上千之得一千六百二十寸為一斛積寸下退一等得一百六十二寸為一鬥積寸倍之得三百二十四寸。為二鬥〉

　　〈積寸以腹修五寸約之得六十四寸八分乃以十二乘之得積七百七十七寸六分。又以開方除之得圓周二十七寸餘四十八寸六分倍二十七〉

　　〈從方法。得五十四。下法一亦從方法得五十五以三除二十七寸得九寸又以三除不盡四十八寸六分。得一十六寸二分與法俱上十之是為壺〉

　　〈腹徑九寸。五百五十分寸之一百六十二母與子亦可俱半之為二百七十五分寸之八十一。淳風等。按其問宜雲。今有壺腹修五寸容鬥五升三〉

　　〈分益一則為二鬥。得圓囷之象。問積寸之與周徑各幾何曰。積三百二十四寸。週二尺七寸。二百七十五分寸之二百四十三徑九寸二百七十五〉

　　〈分寸之八十一。術宜雲。置二鬥以鬥法乘之得積寸。以腹修五寸除之所得以十二乘之。開方除之得周數。三約之即得徑數。〉

　　〈楊輝摘奇演算法九章。立方積內原有分母開方術曰置全積通分並分子為實。開立方除得面積扵上。別置積內原分母如立方而一為法以〉

　　〈除。求出面積即得所答方面全步幾分之幾楊輝纂類賈憲立成釋鎻立方法曰置積為實。別置一算名曰下法。於實數之下自末至首常超〉

　　〈二位。上商置第一位得數下法之上亦置上商又乘置平方命上商除實訖。取用第二位法。三因平方一退。亦三因從方面二退為廉。下法三〉

　　〈退。續商第二位得數。下法之上亦置上商為隅。以上商數乘廉隅。命上商除實訖。求第三位。即如求第二位取用。〉

　　〈九章算經今有積一百八十六萬八百六十七尺。此尺。謂立方尺也。凡物有高深深而言積者曰立方問為立方幾何。〉

　　〈答曰一百二十三尺。楊輝詳解今問積中第一位是一立方自方百尺。第二位有三平方。各〉

　　〈方一百尺高二十尺其三廉各長一百尺。方二十尺。其一隅立方二十尺第三位積有三平方各方一百二十尺。高三尺。及三廉各長一百一〉

　　〈十尺。方三尺。其一隅立方三尺解題方自乘名為平方。又以方乘平方名曰立方狀如骰子取用勾深致遠之算。立方法曰。賈憲細草編為〉

　　〈活法置積為實別置一算名曰下法。原下之法於實數之下自末至首常超二位約實原乘之法過二位今還源故超二位一下定一。千下定〉

　　〈十百萬下定百上商置第一位得數以方數為主。自乘求商。不𣣔迭注。詳見細草下法之上亦置上商即平方面又乘為平方命上商除實訖。〉

　　〈除去一立方也三因平方一退亦三因從方面。二退為廉第一位得數乃立方其第二位有三個廉一小隅為助三因方廉退方一廉二者蓋〉

　　〈其數有等第也下法三退原超二位今退三位。以定上商續商第二位得數下法之上亦置上商為隅第二位中隅見在解以上商數乘㢘隅〉

　　〈以平乘高命上商除實訖第二位取用如此求第三位即依第二位取用以上商乘廉三因隅法併入為方又以方法之下複置上商三因為〉

　　〈廉其方法一退㢘法再退下法三退續商第三位得數下法之上亦置上商為隅三因廉法隅自乘之皆命上商除實見第二位解適盡合問〉

　　〈草曰置積一百八十六萬八百六十七尺為實。別置一算名曰下法於實數之下自末位常超二位約實。一下定一千下定十百萬下定百〉

　　〈上商置第一位得數實數一百萬上商置一百原定百也下法之上亦置上商一百乘為平方一百乘一百得一萬尺乃命上商一百除實一〉

　　〈百萬尺三因平方一退為三萬尺。亦三因從方二退為廉三百尺下法三退定十續商置第二位得數二十下法之上亦置上商為隅二十以〉

　　〈上商乘廉得六千隅得四百。命上商除實訖。余一十三萬二千八百六十七尺以上商二十乘廉得一萬二千尺三因隅法得一千二百尺並〉

　　〈入方一退共四萬三千三百尺。方法之下複置上商一百二十三因為廉三百六十廉法二退下法三退續商置第三位得數三尺下法之上〉

　　〈亦置上商為隅三尺。以上商乘廉一千八十。隅九尺。皆命上商除實適盡合問。增乘方法。立方原是乘而又乘至數。今以增乘為除求源草〉

　　〈曰。實上商置第一位得數一百。以上商乘下法置廉一百。乘廉為方一萬除實訖複以上商一百乘下法入廉共二百乘廉入方共三萬。又乘〉

　　〈下法入廉共三百其方一廉二。下三退定十再扵第一位商數之次複商第二位得數二十以乘下法入廉。共三百二十乘廉入方。共三萬六〉

　　〈千四百命上商除實訖餘一十三萬二千八百六十七。複以次商二十乘下法入廉共三百四十乘㢘入方共四萬三千二百尺。又乘下法入〉

　　〈廉共三百六十其方一廉二下三退如前。上商第三位得數三尺乘下法入廉共三百六十三乘廉入方共四萬四千二百八十九。命上商三〉

　　〈尺除實適盡得立方一面之數。九章算經又有積一千九百五十三尺。八分尺之一問為立方幾何。〉

　　〈答曰一十二尺半。今有積六萬三千四百一尺五百一十二分尺之四百四十七。問為立方〉

　　〈幾何答曰三十九尺八分尺之七。〉

　　〈楊輝詳解解題此是帶予立方。分母子立方法曰。置積以分母通其全。加內子為實。通分之意。開立方除之。前術得積。多分母子一叚。未可便〉

　　〈見方面。別置分母。如立方而一為法。母先曾乘而又乘。故如立方而一。除積還源。得立方一面之數。草曰。置積。以分母五百十二通全。六萬〉

　　〈三千四百一尺。加內。子四百四十七為實。得三千二百四十六萬一千七百五十九。開立方除之為積。得三百一十九。別置分母五百十二。如〉

　　〈開立方而一為法得八除積三百十九。得立方一面之數。前答。嚴恭通原算法術曰。置積以分母相乘納子。三千二百四十六萬一千七百五〉

　　〈十九分為積實。開立方除。借一算為下隅。常超二位約實。上商三百乘下隅得三百為廉法。以上商三百與廉三百乘得九萬為方法。與上商〉

　　〈三百呼除本積三九除去二千七百萬。餘積實存五百四十六萬一千七百五十九分為實。三因廉得九百。三因方得二十七萬。續上商一十〉

　　〈乘下隅得一十。卻乘廉九百得九千。併入方法。又以上商一十。乘下隅一十得一百。亦併入方法共二十七萬九千一百分為方法。與上商一〉

　　〈十呼除本積一二除去二百萬。再呼一七除去七十萬。一九除去九萬。一一除去一千。余積存二百六十七萬七百五十九分為實。以扵方法〉

　　〈內更加原廉九千。又倍商乘隅得二百併入方法。次以上商三百一十三因得九百三十為廉法。續上商九分乘下隅得九分。卻乘廉得八千〉

　　〈三百七十併入方法。又上商九分乘下隅九分。得八十一分亦併入方法。共二十九萬六千七百五十一分為方法。與上商九分呼除本積二〉

　　〈九除去一百八十萬。再呼九九。除去八十一萬。六九除去五萬四千。七九除去六千三百五九除去四百五十。一九除去九分適盡。得三百一〉

　　〈十九分為實。次置分母五百一十二。亦以開立方除之得八為法。實如法而一合前問。〉

　　〈今有積一百九十三萬七千五百四十一尺。二十七分尺之一十七。問為立方幾何。〉

　　〈答曰。一百二十四尺。太半尺開立方。立方適等求其一而也。術曰。置積為實借一算步之超二等。言〉

　　〈千之面十。言百萬之面百。議所得以再乘所借一算為法而除之。再乘者。亦求為方幕以上議命而除之。則立方等也。除已。三之為定法。為當〉

　　〈複除。故豫張三面以定方羃為定法也。複除折而下複除者。三面方羃以皆自乘之數。須得折議定其厚薄爾。開平羃者。方百之面十。開立羃〉

　　〈者。方千之面十據定法也。有成方之羃故複除當以千為百。折下一等也。以三乘所得數。置中行設三廉之定長複借一算置下行。欲以為隅〉

　　〈方。立方等未有定數。且置一𥮅定其位步之中超一下超二位。上方法長自乘而析。中廉法但有長故降一等。下隅法無面長故又降一等也。〉

　　〈複置議以一乘中。為三廉備羃也。再乘下令隅自乘為方羃也。皆副以加定。法以定除。三面。三廉。一隅。皆已有羃。以上議命之。而除去三袤之〉

　　〈厚也。也除已。倍下並中從定法。凡再以中三以下加定法者三廉各當以兩面之羃。連于三廉之端。以待複除也。言不盡意。解此要當以棊乃得〉

　　〈明耳。複除折下。如前開之。不盡者亦為不可開術亦有以定法命分者。不如故羃。開方以微數為分也。若積有分者。通分內。子為定實。定實乃〉

　　〈開之訖。開其母以報除。淳風等。按分母可開者並通之積。先合三母。既開之後。一母尚存。故開分母求一母為法。以報除也。若母不可開者。又〉

　　〈以母再乘定實。乃開之訖。令如母而一。淳風等。按分母不可開者。本一母也。又以母再乘之。今合三母。既開之後。一母猶存。故令一母而一得〉

　　〈全面也。按開立方。知立方適等求其一面之數。借一算步之超二位者。但立方求積。方再自乘。就積開之。故超二位。言千之面十。言百萬之面〉

　　〈百。議所以再乘所借算為法而以除。知求為方羃以議命之而除。則立方等也。除已。三之定注為積。未盡當複更除。故豫張三面已定方羃為〉

　　〈定法複折除而下。知三面方羃。皆以有自乘之數。須得折議定其厚薄。據開平方百之面十。其開立方即千之面十。而定法已有成方之羃。故〉

　　〈複除之者當以千為百。折下一等。以三乘所得數置中行者設三廉之定長。複借一算置下行者。欲以為隅方。立方等未有數。且置一算定其〉

　　〈位也。步之中超一下二者。上方法長自乘而一折中。廉法但有長故降一等。下隅法無面長。故又降一等。複置議以一乘中者。為三廉借羃再〉

　　〈乘下當令隅自乘為方羃。皆副以加定法。以定法除者。三面。三廉。一隅。皆已有羃以上議命之而除去三袤之厚。除已倍下並中從定法者三〉

　　〈廉。各當以兩面之羃連于兩方之面一隅連于三廉之端以待複除其開之不盡者折下如前開方即合所問有分者通分納子開之訖開其〉

　　〈母以報除可開者以通之積。先合三母。既開之複一母尚存。故開分母者求一母為法以報除若母不可開。者又以母再乘定實。乃開之訖。令〉

　　〈如母而一。分母不可開者本一母又以母再乘令合三母。既開之複亦一母尚存故令如母而一得全面。也。〉

　　〈透簾。細草今有立方積四千九百八十三萬六千三十二尺。問立方一面多少〉

　　〈答曰三百六十八尺法曰開立方除之舊草冗繁今以透廉開之草曰列積為實。借一算〉

　　〈子名立隅又名約法常超二位約實兩度進上合商三百。三因立隅得三百萬別置為廉法又三因得九百萬為方法只以方法命商除實二〉

　　〈千七百萬三因方法為二千七百萬一退三因廉得九百萬二退。立隅法三退續商六十寸廉法內添隅添立隅六千共九萬六千。六因加入〉

　　〈方法得三百二十七萬六千命續商除實。餘有三百一十八萬三十二。在廉法內更添隅法六千得十萬二千六因加入方法得三百八十八〉

　　〈萬八千一退廉法內又添六千共十萬八千二退。下法三退續商八寸。廉法內添隅法八寸共一千八十八乃八因加入方法得三十九萬七〉

　　〈千五百四寸命商八寸除實恰盡嚴恭通原算法術曰。置本積為實。借一算為下隅常超二位約實上商二百尺乘下隅得三百尺為廉法。以〉

　　〈上商三百尺與廉三百尺相乘得九萬尺為方法。與上商呼除本積三九除去二千七百萬。餘積上存二千二百八十三萬六千三十二尺為〉

　　〈實。三因廉得九百尺。三因方得二十七萬尺。續上商六十尺乘下隅得六十尺。卻乘廉得五萬四千尺併入方法。又上商六十尺與下隅六十〉

　　〈尺相乘得三千六百尺亦併入方法。共三十二萬七千六百尺為方法。與上商六十尺。呼除本積三六除去一千八百萬。再呼二六除去一百〉

　　〈二十萬。再呼六七除去四十二萬。再呼六六除去三萬六千尺。餘存三百一十八萬三十二尺。再于方法內更加原廉五萬四千尺。又倍商隅〉

　　〈三千六百得七千二百尺。亦併入方法共三十八萬八千八百尺。次以上商三百六十三因得一千八十為廉法。續上商八尺乘下隅得八尺。〉

　　〈卻乘廉得八千六百四十。又上商八尺與下隅八相乘得六十四尺。亦併入方法共三十九萬七千五百四尺為方法。與上商八尺呼除本積〉

　　〈三八除去二百四十萬。再呼八九除去七十二萬。再呼七八除去五萬六千。再呼五八除去四千尺再呼四八除去三十二尺適盡。得立方面〉

　　〈三百六十八尺合前問。丁巨演算法今有積一萬五千六百二十五尺。問為立方一面幾何。〉

　　〈答二十五尺。置積尺。以一算於五尺之下常超二位。至位之下。上商二。呼一二生廉〉

　　〈二二二生方四。呼二四如八去積八千尺。餘七千六百二十五尺。呼一二添廉二二四添方八又呼一二添廉二。方法一退。廉法二退。下法三〉

　　〈退上商五。呼五六生方三十五五生方二十五。命商除積。一五如五去積五十尺五五二十五去積二千五百尺。二五一十去積一百尺。五五〉

　　〈二十五去積二十五尺適盡。嚴恭通原演算法今有積四萬六千六百五十六尺。問立方面若干。〉

　　〈答曰。三十六尺。術曰。置本積為實。借一算為下隅常超二位約實。上商三十尺。乘下隅〉

　　〈得三十尺為廉法。以上商三十尺與廉三十尺相乘得九百尺為方法。與上商呼除本積。三九除去二萬七千尺。余積實存一萬九千六百五〉

　　〈十六尺為實。再以三因廉得九十尺。三因方得二千七百尺。續上商六尺乘下隅得六又卻乘廉得五百四十尺併入方法。又上商六尺。與下〉

　　〈隅六尺相乘得三十六尺亦併入方法。共三千二百七十六尺為方法。與上商六尺呼除本積三六除去一萬八千。再呼二六除去一千二百。〉

　　〈再呼六七除去四百二十。再呼六六除去三十六尺適盡。合前問。今有積七億尺。問立方面若干。〉

　　〈答曰。八百八十七尺。二百三十六萬二千九百六十九分尺之二百一十三萬五千八百九十七。〉

　　〈術曰。置本積為實。借一算為下隅常超二位約實。上商八百尺。乘下隅得八百尺為廉法。以上商八百尺。與廉八百尺。相乘得六十四萬尺為〉

　　〈方法。與上商呼除本積。六八除去四億八千萬。再呼四八除去三千二百萬。餘積實存一億八千八百萬尺為實。三因廉法得二千四百尺。三〉

　　〈因方得一百九十二萬。續上商八十尺。乘下隅得八十尺。卻乘廉得一十九萬二千併入方法。又上商八十尺。與下隅八十尺。相乘得六千四〉

　　〈百尺亦併入方法。共二百一十一萬八千四百尺為方法。與上商八十呼除本積。二八除去一億六千萬。再呼一八除去八百萬。再呼一八除〉

　　〈去八十萬再呼八八除去六十四萬。再呼四八除去三萬二千。餘積實存一千八百五十二萬八千尺為實。次於方法內更加原廉一十九萬〉

　　〈二千又倍商乘隅得一萬二千八百亦併入方法。共二百三十二萬三千二百。次以上商八百八十三。因得二千六百四十為廉法。續上商七〉

　　〈尺乘下隅得七尺卻乘廉得一萬八千四百八十併入方法。又上商七尺。與下隅七尺。相乘得四十九尺亦併入方法。共二百三十四萬一千〉

　　〈七百二十九尺為方法。與上商七尺呼除本積。二七除去一千四百萬。三七除去二百一十萬。四七除去二十八萬。一七除去七千。七七除去〉

　　〈四千九百二七除去一百四十。七九除去六十三尺。餘積存二百一十三萬五千八百九十七尺。又于方法內更加原廉一萬八千四百八十。〉

　　〈又倍商乘隅得九十八尺亦併入方法。次又以上商八百八十七尺。三因得二千六百六十一尺。更加原借一隅算亦併入方法。是得方面八〉

　　〈百八十七尺。二百三十六萬二千九百六十九分尺之二百一十三萬五千八百九十七。合前問。〉

　　〈今有積七億二千一百七十三萬四千二百七十三尺。問立方面若干。答曰。八百九十七尺。〉

　　〈今有積七十億尺。問立方若干。答曰。一千九百一十二尺。一千九十七萬二千九百六十九分尺之〉

　　〈一千二十一萬七千四百七十二。今有積八十億尺。問立方面若干。〉

　　〈答曰。二千尺。術曰。俱以前開立方除之即得。〉

　　〈楊輝纂類開立圓者。先以方法十六乘積。如圓法九而一開立方除之。積有分母子者通。母內子立圓用十六乘九除。開立方除之得積。別置分母〉

　　〈如立方而一。為法除積求之。增乘方法曰。實上商置第一位得數。以上商乘下法置廉。乘廉為方除實訖。複以上商乘下法入廉。乘廉入方。又乘下〉

　　〈法入廉其方一廉二。下三退。再扵第一位商數之次。複商第二位得數以秉下法入廉乘廉入方命上商除實訖。複以次商乘下法入廉。乘廉入方〉

　　〈又乘下法入廉其方一廉二。下三退。如前。上商第三位得數。乘下法入廉乘廉入方命上商除實適盡得立方一面之數。〉

　　〈九章算經今有積四千五百尺。亦謂立方之尺也。問為立圓徑幾何。答曰二十尺依宻率立圓徑二十尺。計積四千一百九十尺。二十一〉

　　〈分尺之一十今有積一萬六千四百四十八億六千六百四十三萬七千五百尺。問為〉

　　〈立圓徑幾何。答曰一萬四千三百尺依宻率為徑一萬四千六百四十三尺。四分〉

　　〈尺之三術曰置積尺數以十六乘之九而一所得開立方除之即九徑。立圓即〉

　　〈九也。為術者蓋依週三徑一之率令圓羃居方羃四分之三圓囷居立方亦四分。之三更令圓囷為方率十二為丸率九丸居圓囷又四分之〉

　　〈三也置四分自乘得十六三分自乘得九。故丸居立方十六分之九也。故以十六乘積九而一。得立方之積。丸徑與立方等。故開立方而除得〉

　　〈徑也。然此意非也。何以驗之取立方綦八枚。皆令立方一寸。積之為立方二寸。規之為圓囷徑二寸。高二寸。又複橫因之則其形有似牟合方〉

　　〈蓋矣。八棊皆然。似陽馬圓然也按合蓋者。方率也。丸居其中即圓率也推此言之。謂夫圓囷為方率豈不闕哉。以週三徑一為圓率。則圓羃傷〉

　　〈少。令圓困為方率。則丸積傷多。互相通補。是以丸與十六之率。隅與實相近而丸猶傷多耳。觀立方之內。合蓋之外。雖衰殺有漸。而多少不掩。〉

　　〈判合緫結。方圓相纏。濃纖詭互。不可等正。欲陋形措意。懼失正理。敢不闕疑以俟能言者。黃金方寸重十六兩。金丸徑寸重九兩。率生於此。〉

　　〈未曾驗也周官考工記𣓨氏為董叚煎金錫則不耗不耗然後權之。權之然後凖之凖之然後量之言煉金使極精而後分之。則可以為率也〉

　　〈今丸逕自乘三而一開方除之。即丸中之立方也。假令丸中立方五尺。五尺為勾勾自乘羃二十五尺倍之得五十尺。以為股羃。謂卑面方五〉

　　〈尺之弦也。以此弦羃為股。亦以五尺為勾。並勾股羃得七十五尺。是為大弦羃。開方除之。則大弦可知也。大弦則中立方之長邪。邪即九徑。故〉

　　〈中立方自乘之羃。於九逕自乘之羃三分之一也。今大弦還乘其羃。即丸外立方之積也。大弦羃開之不盡。令開羃七十五。再自乘之為面。命〉

　　〈得外立方積四十二萬一千八百七十五尺之面。又令中立方五尺自乘。又以方乘之。得積一百二十五尺。一百二十五尺自乘為面。勾得積〉

　　〈一萬五千六百二十五尺之面。皆以六百二十五約之。外立方積六百七十五尺之面。中立方積二十五尺之面也。張衡算。又謂立方為質。〉

　　〈立圓為渾。衡言質之與中外之渾六百七十五尺之面。開方除之不足一。謂外質積二十六也內渾二十五之面。謂積五尺也。今微令質言中〉

　　〈渾。渾又言質則。質相與之率。猶衡二渾相與之率也。衡蓋亦先二質之率。推以言渾之率也。衡又言質六十四之面渾二十五之面。質複言〉

　　〈渾。謂居質八分之五也又雲方八之面圓。圓渾相推知其複以圓囷為方率。渾為圓率也失之遠矣衡說之自然欲恊其陰陽奇偶之說而不〉

　　〈顧疏宻矣。雖有文辭。斯亂道破義病也。置外質積二十六。以九乘之。十六而一。得積十四尺八分之五即質中之渾也。以分母乘全內子。得一〉

　　〈百一十七。又置內質積五。以分母乘之得四十。是謂質居渾一百一十七分之四十。而渾率猶為傷多也。征令方二尺。方四面並得八尺也。謂〉

　　〈之方周其中今圓徑與方等亦二尺也。丸半徑以乘圓周之半即圓羃也。半方以乘方同之半即方羃也。然則方周如方羃之率也。圓周知圓〉

　　〈羃之車也。按如衡術。方周率八之面。圓周率五之面也。今方週六十四尺之面。即圓周四十尺之面也。又令徑二尺自乘得徑四尺之面。是為〉

　　〈圓周率十二之面。而徑率一之面也。衡亦以週三徑一之率為非。是故更著此法。然增周太多過其實矣。淳風等。按祖暅之謂劉徽。張衡。二〉

　　〈人皆以圓囷為方率。丸為圓率。乃設新法。祖暅之間立圓術曰。以二乘積。開立方除之即立圓徑。其意何也。取立方棊一枚。令立樞扵左後之〉

　　〈下隅。從規去其右上之廉。又合而橫規之。去其前上之廉。於是立方之棋分而為四規。內棋一謂之內棊規。外棊三謂之外棊規。更合四棊後〉

　　〈橫斷之。以勾股言之。令余高為勾。內棊斷上方為股本方之數其弦。勾股之法以勾羃減弦羃。則餘為股羃。若令余高自乘減本方之羃。餘即〉

　　〈內減其斷上方之羃也。本方之羃。即外四棊之斷上羃。然則余高自乘即外三棊之斷上羃矣。不問高卑勢加然也。然固有所歸同而途殊者〉

　　〈爾。而乃控遠以演類。借況以析𢕄。按陽馬方高數參等者列而立之。橫截去上則高自乘。與斷上羃數亦等焉。夫迭棊成立積。緣羃勢既同。則〉

　　〈積不客異。由此觀之。規之外三棊旁蹙為一。即一陽馬也。三分立方。則陽馬居一。內棊居二可知矣。合八小方成一大方。合八內棊成一合蓋。〉

　　〈內棊居小方三分之二。則合蓋居立方亦三分之二。較然驗矣。置三分之二。以圓羃率三乘之。如方羃率四而一。約而定之以為九率。故曰九〉

　　〈居立方三分之一也。等數既宻。心亦昭晰。張衡放舊。貽哂於後。劉徽循故。未暇校新。夫豈難哉。抑未之思也。依率立此圓積。本以圓徑再自乘。〉

　　〈十一乘之。二十一而一約此積。今欲求其本積。故二十一乘之。十一而一。凡物再自乘開立方除之。複其本數。故立方除之即九徑也。〉

　　〈楊輝詳解積一百六十四萬四千八百六十六尺四寸三分七厘五毫。問為立圓徑幾何。〉

　　〈答。一百四十三尺。解題立圓其狀如球。居立方十六分之九。立圓法曰。以方法十六乘積。〉

　　〈如圓法九而一為實。平圓居平方四分之三。更添一乘為立圓立方。其立圓居立方十六分之九。取以為法十六乘。九而一。即互換之意。開增〉

　　〈乘立方除之前注草曰。置積題數以方法十六乘之。以九除之為實。得二百九十二萬四千二百七尺開增乘立方除之。立草在九章卷〉

　　〈首佈置圓內透簾細草今有立方圓積九百二十七寸。問徑多少。〉

　　〈答曰一尺二寸法曰。置積寸以十六乘之九而一得一千七百二十八寸為實。開立方〉

　　〈除之即得。合問草曰十六乘之九除者。添入角積也。改立圓為立方是以開立方見一面數。。丨隅法三進在千之下。置廉一千。方一〉

　　〈千。除實一千方三因一為三千一退廉三因得三千二退。下位三退。續商二寸廉法內添隅法二寸得三十二寸。二因添入隅法得三百六十〉

　　〈四。命商除實盡也今有立方。圓平方各一所共計積二十二萬九千六百七尺。只雲立方面〉

　　〈多如立圓徑七尺其平方面如立圓徑三分之二。問三事各多少。答曰。立方面五十五尺。立圓徑四十八尺。平方面三十二尺。〉

　　〈法曰。以立方開之。草曰。置共積二十二萬九千六百七尺在地。於頭位以多七尺自乘得數。又以七尺再乘之得三百四十三尺減扵頭位〉

　　〈共積餘有二十二萬九千二百六十四。又以一百四十四為分母乘之。頭位共得三千三百一萬四千一十六尺為實置於頭位。又多數七尺〉

　　〈自乘得數以四百三十二乘之得二萬一千一百六十八尺為從法。又多七尺乘四百三十二得三千二十四。又添入六十四共得三千八十〉

　　〈八為廉常。以二百二十五為隅。立方開之。計積為實三千三百一萬四千一十六於頭位。從法二萬一千一百六十八扵下位廉法三千八十〉

　　〈八於從法下。隅法二百二十五于廉之下。從法一進。廉法二進。隅法三進上商四共隅法相呼四因廉法得一百二十萬八千八百。廉法相呼〉

　　〈生於從法得五百四萬六千八百八十。命商除之。餘有一千二百八十二萬六千四百九十六。又四因隅法生於廉法得二百一十萬八千八〉

　　〈百。又生於從法得一千三百四十八萬二千八十。又四因扵廉法得三百萬八千八百又八因隅法一退于廉得三百一十八萬八千八百。從〉

　　〈法一退廉法二退隅法三退上商八生於廉法得三萬一千八百八十八又八生扵從法得一百六十萬三千三百一十二命商除之恰盡。得〉

　　〈立圓徑內加七尺為立方面二因三除為平方面也合問今有圓球一。只徑一尺二寸問計積寸多少〉

　　〈答曰。九百七十二寸。法曰。徑再自相乘得一千七百二十八寸。又以九之。如十六而一。得積〉

　　〈寸合問。草曰徑再自相乘為立方比立圓球子多四角積寸。一十六分之九。立圓積是十六分之九。先九因而後十六除者。恐有不盡免通分也。〉

　　〈嚴恭通原演算法今有積二十六萬六千九百三十五尺半。欲為立圓。問徑若干。答曰。七十八尺。〉

　　〈術曰。置本積以十六乘之。得四百二十七萬九百六十八尺。九除之得四十七萬四千五百五十二尺為實。以開立方除。借一算為下隅。常超〉

　　〈二位約實。上商七十尺乘下隅得七十尺為廉法。以七十尺與上商七十尺相乘得四千九百尺為方法。與上商七十尺呼除本積。四七除去〉

　　〈二十八萬七九除去六萬三千。餘積實存一十三萬一千五百五十二尺為實三因廉得二百一十尺。三因方得一萬四千七百尺。續上商八〉

　　〈尺乘下隅得八尺。卻乘廉得一千六百八十尺併入方法。以上商八尺乘下隅得六十四尺亦併入方法。共一萬六千四百四十四尺為方法。〉

　　〈與上商八尺呼除本積。一八除去八萬。六八除去四萬八千。四八除去三千二百四八除去三百二十。四八除去三十二適盡。得圓徑七十八〉

　　〈尺合前問。今有積七百三十五萬七千五百尺。欲為立圓。問周若干。〉

　　〈答曰。七百六尺。一百四十九萬七千四百二十七分。尺之一百二十六萬四千一百八十四。〉

　　〈術曰置積以一百四十四乘得一十億五千九百四十八萬。又三除之。得三億五千三百一十六萬尺為實。以前開立方除之即得。〉

　　〈楊輝詳解積一百三十三萬六千三百三十六尺。問為三乘方幾何。答曰。三十四尺。〉

　　〈解題三度相乘。其狀匾直逓增三乘開方法草曰。上商得數下法增為立方除實即原乘意。置積為實。別置一算名曰下法。扵實末常超三位〉

　　〈約實一乘超一位三乘超三位。萬下定實上商得數三十。乘下法生下廉三十乘下廉生上廉九百乘上廉生立方二萬七千。命上商除實。餘〉

　　〈五十二萬六千三百三十六。作法商第二位得數。以上商乘下法入下廉共六十。乘下廉入上廉共二千七百。乘上廉入方共一十萬八千。又〉

　　〈乘下法入下廉共九十乘下廉入上廉共五千四百。又乘下法入下廉共一百二十方一上廉二下廉三下法四退。方一十萬八千。上廉五千〉

　　〈四百下廉一百二十。下法定一又于上商之次續商置得數第二位四。以乘下法入廉一百二十四乘下廉入上廉共五千八百九十六。乘上〉

　　〈廉並為立方一十三萬一千五百八十四命上商除實盡。得三乘方一面之數如三位立方。依第二位取用又術曰兩度開平方開第一次〉

　　〈平方得一千一百五十六。開第二次平方得三十四。〉

　　永樂大典卷之一六千三百四十四

學達書庫(xuoda.com)