圖書集成·日月部匯考二

日月部匯考二

　　▼明，湯若望《新法曆引》

　　《交食》

　　凡日月之行二十九日有奇，而東西同度，謂之「會朔。」至若日行在黃道近交，人視為與日同經同緯，是人目與日月相參直，而月魄正隔日光，於人目則為日食。日食者，非日失其光，光為月掩耳。凡太陰距太陽百八十度，而正與之沖，謂之望。若當沖時，月行近於兩交，必入地景而為暗虛。此乃日月同在一線，而地居其中間，日光為地所阻，不能射照月體，則月失其光而為月食。此日月二食者，躔度有恆，持籌推步，分秒確然，而曆家各法之疏密，於此更難掩也。試言其略，黃白二道相交之二所，名「正交、中交。」凡日月行及二交為同度，同度則有食矣。然而論交又須論限，及交而在限內則食，限外則不食，此不可不審也。顧限度諸方不一，蓋太陽于諸方之地，平高度不同，而陰陽二曆之各限亦異。論暖帶下之地，二曆互相受變。

　　如白道向南極半周，有時在天頂及黃道之中，勢必反謂為陰曆；白道向北半周，是時在黃道外，勢必反謂為陽曆。故其下日食之限，莫得而定之也。他域更近於北，必陰曆限多，陽曆限少；更近于南，必陽曆限多、陰曆限少。比如京師近北，約算陽曆八度、陰曆二十一度，則知日月相會。凡在陽曆近二交八度，在陰曆近二交二十一度，其下必見日食。而過此限以往，則否，即北可以推南，莫不以遠近分多寡矣。然而二曆食限之度有異者，其故蓋在月輪。月輪比日最近於地，而月又小於地。人目見月之所又在地面，不在地心，故以月天論地平。雖天與地球皆為平分，直過其心，而人在地面高，所以視天地之兩界，則似地球與月天，非平分也。少半在上，多半在下，而差約一度。

　　故以本法推算，月已出正地平，其於人目所視之地平，尚少一度。此其較謂之「視差。」蓋惟月在天頂正地平與視地平之極，皆以一直線合於天頂，無有視差。

　　過此左右，不免有差。愈遠天頂愈近，地平差必愈甚。

　　夫視差無他，恒降下月體數十分耳。設令日月同度，同在近交之南，又因同度並在正地平上高二十度，則太陽于視地平為十九度五十八分，祇降二分，太陰于視地平為十九度，直降一度矣，而日月二差之較為五十八分。故以算論，雖二曜同高同度，而人目視之，太陰恒下于太陽，一度弱，不掩日光則不食。若二曜在地平上高七十度，則太陽無視差。太陰視差止二十分，其降於太陽亦止二十分，勢必相切，或至掩數分而成食。若二曜在交北，又當乙太陰算在太陽之上，庶因視差所降，而掩陽光以為食也。顧此二地平之差，又分二類：一加減交食分數，謂之氣差；一加減時刻，謂之時差。曆算之艱且劇，莫過於此，所最當究心者也。

　　日食之全與不全，其故有二：一由天上之行，一由食時地平上高弧之度，故均一食也。有見全食者，有見食多寡不等者，有全不見食者。就南北論，見食地界，設如北京見全食，其南北各距四十五度之地，為萬一千有餘裡，皆見有食，然而多寡不等。就東西論，各距六十度為萬五千有餘裡，各見食而分數多寡亦不等焉。即月食時刻，南北亦有不同，而東西為甚也。

　　▼《渾天儀說》

　　《太陽及太陰本行合宗動之驗》

　　太陽為時日之原。一日約東行一度，于黃道為正，而於赤道恒為斜。或在兩道之交，或北上，或南下，絕無定居，故無一定之時。此四季所繇以變易也。迨加以宗動，即見其出沒之廣不一，晝夜之長短有變。如日在降婁初度為春分，則出正東，沒正西，晝與夜皆等。

　　自此以往漸斜去赤道北，出沒較前為廣矣。晝長而夜短，至夏至為最矣。乃從夏至而退行一度，其出其沒，其晝其夜，與前所得等，漸退行，漸與前等。惟過秋分而太陽行赤道南，則於前後相對，宮度有定比例，彼之所廣，此之所狹，彼之所長，此之所短，若相背而馳者然。

　　太陰依本行隨黃道，約二十九日有奇，而與太陽會，故並論《宗動》則出沒之廣，在地平上下之時，皆從赤道緯，仿太陽為則，且無本光借光於日，因體厚不能透所借之光，故依本行距日遠近不等，有時顯全光，有時少顯其光，只至正相望而食于地，景正相會，而能自以其體掩日原光。又依《宗動》使下地視之，時有先後，方位各異。茲有《本論》，聊述一二如此。

　　《求日月食之原》

　　日月地三體，必並居一直線上，始有食。蓋日體恒居一直線之初界，而彼界則月體、地體迭居焉。如月體居界末，則月面之日光食于地景；地體居界末，則地上之日光食于月景。〈月體厚不能透光故〉「但太陽本行恒依黃道中線，而地居天之中心，一為日光所照，則此面受光，彼面必生景，雖所射景與日正對，亦不能越黃道之中線以為規也。乃太陰本行多在黃道內外，大端距日與地所居之直線遠，則朔望無食。」惟出入黃道之處，與日與地相參直在一線上，則朔望必食。試於本儀考之，設太陰在陰。〈黃道北〉《陽曆》：〈黃道南〉距兩交甚遠，任太陽在何宮度，使轉太陰本圈與日體會為朔或正對為望。從而視之，必日月不能與地並居一直線，無緣得食。若移太陰至正交或中交，不拘得何宮度，與日相會或相望，必日月地之體並居一直線，本朔望時雖欲不食，不可得也。

　　▼《測食》

　　《似食實食說》

　　人恒言日食月食矣，輒概混焉。不知月實食日，則似食而實非食也。何者？日為諸光之宗，永無虧損，月星皆借光焉。朔則月與日為一線，月正會於線上，而在地與日之間。月本厚體，厚體能隔日光於下，於是日若無光，而光實未嘗失也，惡得而謂之食？望則日月相對，而日光正照之，月體正受之，人目正視之，月光滿矣。此時若日月正相對如一線，而地體適當線上，則在日與月之間，而地亦厚體厚體隔日光於此面，而射影於彼面，月在影中，實失其所借之光，是為食也。然其食，特地與月之失日光耳。而其光之失，因光在地面與月體之上，地與月互相遮掩耳，日固自若也。總之，日也、月也、地也，使三體並不居一直線，則更無食矣。若食，則日體恒居一直線之界末，而彼界則月體地體迭居焉。月體居界末，則月面之日光食於地影矣。地體居界末，則地之日光食於月影矣。

　　《日食月食辯》

　　夫日食與月食，固自有異。蓋月食天下皆同，而日食則否。日食，此地速，彼地遲，此地見多，彼地見少；此地見偏南，彼地見偏北，無有相同者也。而月食則凡地面見之者，大小同焉，遲速同焉，經候同焉，唯所居不同子午線者，則時刻不同矣。蓋月一入影，失其借光，更無處可見其光也。

　　《因食而知日月地大小之別》

　　問：「日體甚大於月，與地何征？」曰：「昔有人歎世人止憑肉目，不求物理。嘗設喻曰：『日出地時，設有駿馬疾馳，從日始露至全現，亦可馳四裡。縱令日行與馬等速則四裡，而僅見其全，則全體之徑亦必四裡矣。今駿馬一晝夜所馳，於地幾何？最速不過全圍百分之一也。而太陽日一周焉，則其行之疾莫擬也。是則馬之』」四裡，日之行幾千萬裡矣。日體之大，即此微可知也。

　　且日月體之大小，即食可辨。蓋凡物之有形象者，若空中無所障礙，則其體之全體之分，無不出其本象於一直線而至乎界之一點。此凡物皆然，不拘方圓棱角等形，如有物體於此，其基址即物體也，其界點則線之銳角所至，而入人目者也。凡「實體出《銳角》影者，照體必大乎實體，否則其光不能照實體之全面，而使對面銳影之盡處，仍聚合而有光也。」今欲驗日大乎月，可視日食。月居日前而掩其光，是時月邊尚有光，是日體在外。而其象之入人目，非近來自月體，乃遠來自日體也。其線既為角形，則從月體至日體更為廣大，是其角形之銳，從日來目為一點，而中間能包月體有餘，則日體之大於月體，複奚疑哉？

　　今欲知日體大乎地者，觀諸月食可知月之食地，居日前而生角，影掩月體也。當月食時，月體近乎地則入闊，影遠乎地則人銳，影愈遠愈銳，以聚於一點。若此者孰不信日體之大於地體也？設謂日體與地體均，則地影「大小均，為無窮盡之等影。」若言地體大乎日體，則地影必益遠益大，為無窮盡之大影。其影既遠，不獨食諸天之星，必且食諸星之天矣。則每遇望時，月體詎能移於大影之外乎？由此益信月體之小乎地球也。蓋地影益遠益銳，而月食居此。影或有全而久者，則月徑更小於影，而影小於地。故月體地球之大小從可知矣。

　　▼《曆象圖說》

　　日月合朔圖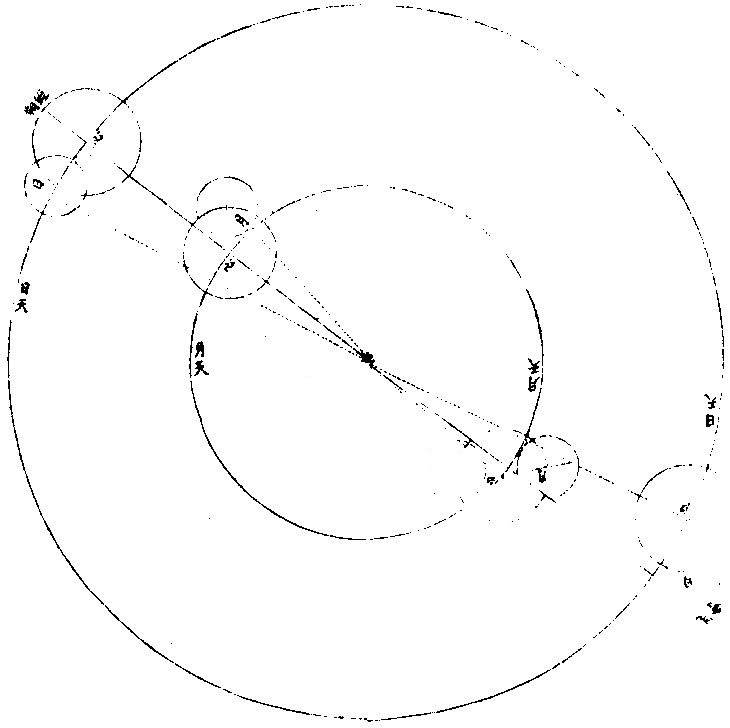

　　

　　日月合朔圖說

　　日月本天，俱包地外，而日遠月近，二天懸殊。又有均輪小輪，高卑遠近，遂與地心不符。自地心出線，上指日月本天，兩均輪心相參，直為經朔。此止就本天之平度，而約其泛曾之日分也。自地心出線，上指日月兩體，徑中心相參，直為「合朔。」此用均輪、小輪上之加減，而定其實會之日分也。弦望加時，星曜同度，其理仿此。

　　月蝕諸象圖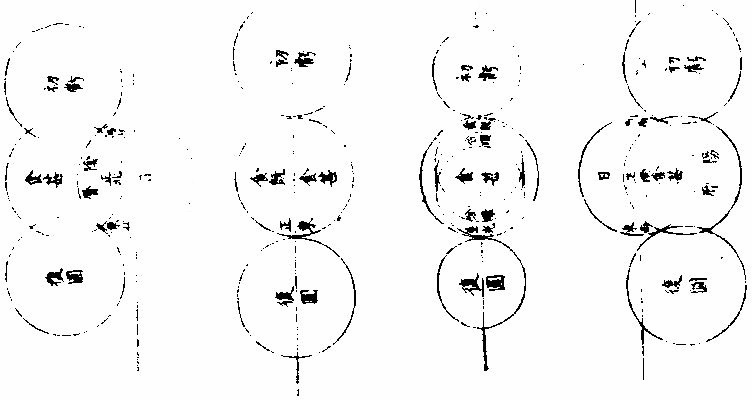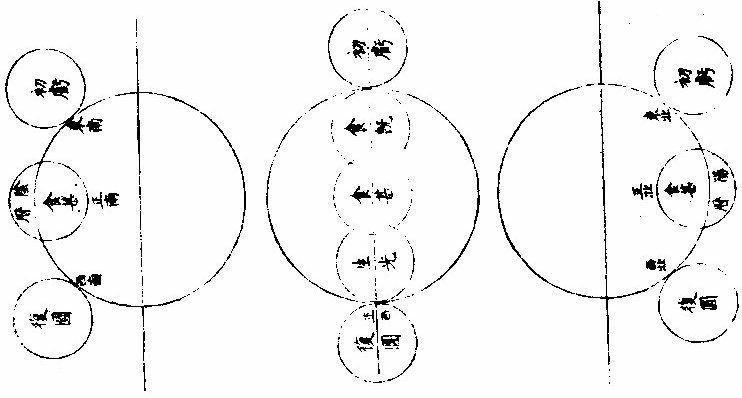

　　

　　交蝕諸象圖說

　　「日月之蝕，皆月之行度使然。日天高而在外，月天卑而在內，周繞大地，相距遠近，時刻不同。合朔而月在日下，則月體掩日；定望而月與日沖，則地隔日光。故日蝕者，月本暗而來掩之也；月蝕者，月入景而不得借光也。月來掩則日為主，而人目所見者即得日光之虧複；月入景則景為主，而人目所見者反得月體之盈虧，此始終方位之所以異也。日為主而月來掩之，故虧起日體之西而複於東，在陽曆則所食偏南，在陰曆則所蝕偏北。景為主而月來就掩，故虧起月體之東而複於西，在陽曆則所蝕偏北，在陰曆則所蝕偏南。」又日月體徑，約略相似，實則日大而月小。日蝕至既，每顯金環，不既者分為三限：月東輪切日西輪，曰初虧，月中徑齊日中徑，曰蝕甚，月西輪切日東輪，曰複圓。蝕既者分為五限。初虧、蝕甚之間，兩西輪齊，曰蝕既。蝕甚、複圓之間，兩東輪齊曰生光。金環者分為七限，蝕既、蝕甚之間，環光自微至著，曰「合環。」蝕甚、生光之間，環暈全而複缺，曰分環。此日蝕之始終也。月徑小於景徑二倍半有奇。每蝕既之後，月行暗中，為時頗久。不蝕既者分為三限：月東輪切景西輪曰初虧，兩中徑齊曰蝕甚，月西輪切景東輪曰複圓。

　　蝕既者，分為五限：初虧、蝕甚之間，兩西輪齊曰蝕既。

　　蝕甚、複圓之間，兩東輪齊曰生光。此月蝕之始終也。

　　總之，月行甚速，經度緯度與日相交相距，是生薄蝕。

　　故日月之蝕，皆由月之行度使然也

　　日月地半徑視差圖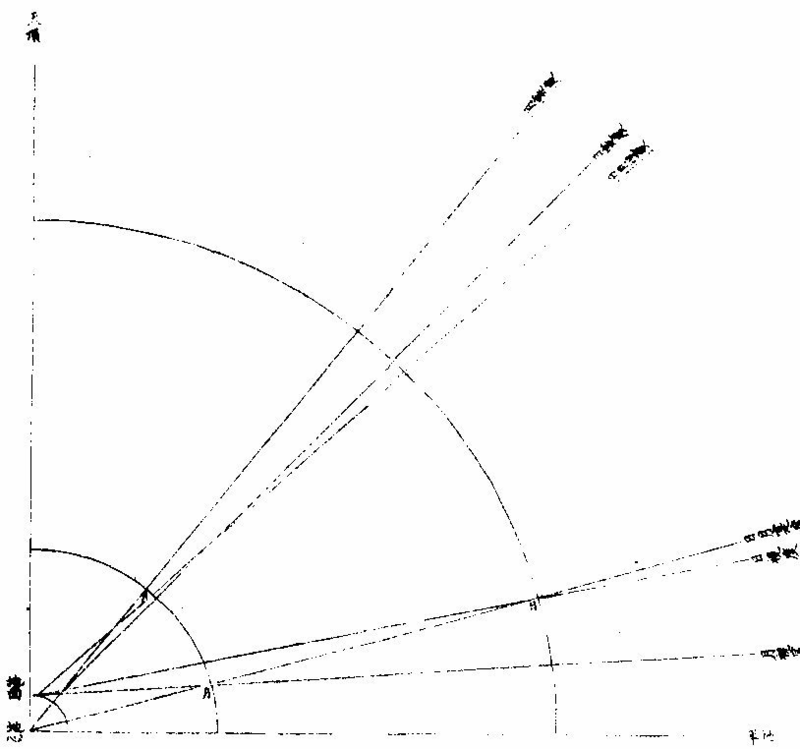

　　

　　《日月地半徑視差圖說》。

　　「曆法屢經修改而漸密，然測候之時，較推步之數，往往未盡合者。古人但知以天定度，未悟以地合天也。

　　地居天中，雖雲微渺，然析其廣輪，則周圍數萬里；計其直徑，則中邊亦萬餘裡，人物環居其上，目力止憑地面所見，而天行樞軸在心，立法必以地心為准，故其差數一生於地勢焉。有地心，有地面，相距為一半」徑，於是從地心而推日月實度所在，又從地面而得日月視度所在，此一端也。一生於天體焉，有日天，有月天，遠近各與地半徑為比例，於是日天遠，而實度與視度之差少，月天近，而視度與實度之差多，此二端也。又一生於地上之高度焉，有地平，有天頂，日月出地，漸升而高，於是近地平則實度與視度之差多，近天頂則視度與實度之差少。大抵漸高漸少，至天頂則無差，此三端也。

　　如下圖地心出直線，指日月實度相合，及地面出直線，指日之視度在實度之下，又指月之視度亦在實度之下，而井在日視度之下。日天遠而月天近，故差不同如此。上圖地面出直線，指日月視度相合，及地心出直線，指日之實度在視度之上，又指月之實度亦在視度之上，而並在日視度之上。日天、月天，遠近不同，故差不同如此。又上圖高而近天頂，視差少，下圖卑而近地平，視差尤多，此差恒降高為卑。測高度者，必于測高內加其時之差，而後得實高。推交會者，必於實會加減其時之差，而後得視會。此差為薄蝕淩犯之至要，而皆地半徑之所生，亦曰《地半徑視差》，亦曰高卑差。

學達書庫(xuoda.com)